Introduction Free-standing film (FSF) has been a wellspring of new liquid crystal science since its discovery in the 1970s, because FSF can consist of a single smectic layer of the single component molecules having bulk liquid crystalline phases. The study of the FSF has been crucial to the current understanding of liquid crystalline phase behavior and it has also addressed an important issue in condensed matter physics, providing a unique experimental condition for the study of phase transitions in two dimensional systems. The FSF is a very interesting object to study, first of all, due to the pronounced surface effects. In addition, the FSF can be regarded as a pure system for studying surface phenomena in liquid crystals. Moreover experimentally, it is much easier to obtain a very thin FSF (with a thickness of less than 1000Å) than a thin liquid crystalline layer held between glass substrates. We studied the optical characteristics of the FSF of a liquid crystal 4-octyl-4’-cyanobiphenyl (8CB) by transmission ellipsometry using a photo-elastic modulator (PEM). Film thickness, layer spacing and anisotropy of the refractive indices of 8CB-FSF were determined from the dependence on the incidence angle of the phase difference between the extraordinary ray and the ordinary ray as follows: the phase differences were simulated by changing the film thickness and the anisotropy of the refractive indices, and then the simulated values were fitted to the experimental results using the least-squares method [1-3]. Molecular dynamics (MD) simulation has been known to be effective to understand the structure and physical properties of matter in the molecular scale. This method has also been applied to the bulk properties of liquid crystals. There have been some research reports on the MD simulation of the adsorbed 8CB molecules on substrates [4, 5]. However, there has been no MD simulation study on the comparison between the bulk and the FSF of 8CB. In this paper, the structural changes with temperature of 8CB-FSF and 8CB-BULK are discussed by the MD simulation. The temperature dependence of order parameter, layer spacing and film thickness are discussed from the simulation results. Liquid Crystal and Simulation Conditions The liquid crystal 8CB discussed in the present paper shows smectic A (SmA) and nematic (N) phases as mesophases [6]. Figure 1 shows the chemical formula and the phase sequence of 8CB. 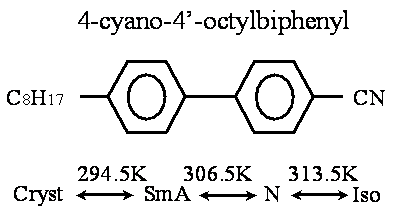
Figure 1. Chemical formula and phase sequence of 8CB. In order to investigate the microscopic behavior of free-standing film (FSF), the molecular dynamics (MD) simulation was carried out for a system which was composed of a liquid crystalline bilayer (64 8CB molecules) and a model atmospheric layer (16 N2 and 4 O2 molecules). Figure 2 shows a snapshot of the initial configuration of 8CB-FSF in a MD simulation cell. For the comparison between FSF and bulk, the MD simulation was also carried out for a system of 64 8CB molecules only, whose initial structure was the same as that of the FSF bilayer. 
Figure 2. Snapshot of the initial configuration of 8CB-FSF in a MD simulation cell. The initial conformation and the partial atomic charges of 8CB molecule were obtained from the molecular orbital calculation for an isolated 8CB molecule (MOPAC2000, PM3, ESP). The initial configuration of molecules in the bilayer was determined based on the quadrupole-pair arrangement [7]. MD simulation was carried out using a software package MASPHYC (Fujitsu Co. Ltd.) [8], which was a multipurpose MD simulator for organic and inorganic materials with a library of various potential functions. MASPHYC has been used for the investigation of the liquid crystalline mesogens, because this package includes some analyzing tools suitable for self-organizing systems [9, 10]. DREIDING parameters were used for calculating the conformational potential due to the chemical bonds [11]. The OPLS parameters were used for calculating the van der Waals interactions between the non-bonded atoms both in the same molecule and in the different molecules [12]. The cut-off radius of such interaction was set to be 10Å. The electrostatic interaction was calculated by the Ewald method based on the aforementioned partial atomic charges. The three dimensional periodic boundary condition was imposed on the FSF system as well as on bulk. In the case of the FSF, however, the boundary condition gave a negligible effect in the direction of the layer normal because the replica 8CB bilayers were separated from the original bilayer by the atmospheric layers whose thickness was much larger than the cut-off radius. The MD simulation was performed in a NTP ensemble. The temperature T was regulated by the Nose algorithm [13]. The pressure P was kept constant at 1 atm by the Parrinello-Rahman algorithm [14]. The time interval was 0.8 fs and the total simulation time was 1.6 ns. It should be noted that the MD simulation in the present paper was carried out without any specific condition for reproducing the FSF. Namely, enforcements such as surface tension and external force were not introduced, and modifications of potential parameters were not performed. Results and Discussion The molecular dynamics simulation was performed for the free-standing film of 8CB (8CB-FSF) and the bulk of 8CB (8CB-BULK). The FSF was successfully reproduced by the ordinary simulation method. The discussion in the present paper mainly focuses on the smectic A phase of the FSF (SmA-FSF) which was experimentally observed in our previous studies [1-3, 15]. Figure 3 shows the time evolution of the orientational order parameter S for 8CB-FSF at 410 K. The S gradually decreases with the time course within 1.2 ns and shows a stationary fluctuation after 1.2 ns. The computer animation illustrated that the molecules are liberated from the initial constraint within 1.2 ns and that they show the thermal motions corresponding to the SmA phase after 1.2 ns. The simulations at the other temperatures also showed such thermal relaxation within 1.6 ns, therefore the analysis of the simulation results was performed based on the snapshots at 1.6 ns. The molecular simulation studies on 8CB [16-18] and the analogues [19, 20] have implied that the outline of the phase formation can be observed mainly within 2 ns and that the precise analysis of detail structures and dynamic properties requires above 5 ns. The simulation for 1.6 ns provides adequate information for examining whether FSF is formed by the ordinary van der Waals interaction, while the further studies with longer simulation time will be required for obtaining the precise phase transition temperatures and for analyzing the molecular motion in detail. 
Figure 3. Time evolution of the orientational order parameter S for 8CB-FSF at 410 K. Figure 4 shows snapshots of 8CB-FSF at the various temperatures. Structures at 300 K and 340 K are those of a crystalline phase. The structures at 380 K and 410 K correspond to the SmA phase which was observed in our previous studies [1-3]. Structures at 420 K, 440 K and 480 K are those of the N phase. At 550 K, the FSF can not exist due to a large isotropic turbulence. These snapshots allow an estimation of the transition temperatures : crystal→SmA is between 340 K and 380 K, SmA→N is between 410 K and 420 K. Since the main purpose of the present paper is to show the existence of the SmA-FSF, the details of the N→isotropic transition, including the existence of the isotropic film, will be discussed in the next work. Only the SmA phase has been observed experimentally for FSF in our previous studies [1-3]. These transition temperatures are higher than those of the bulk (Figure 5) due to the existence of the interfaces between the atmosphere and the liquid crystalline layers (Figure 2) as discussed below. 
Figure 4. Snapshots of 8CB-FSF at various temperatures at 1.6 ns. Figure 5 shows the snapshots of 8CB-BULK. The phase transition temperatures are estimated as follows: crystal→SmA is between 320 K and 330 K, SmA→N is between 340 K and 350 K, and N→isotropic is between 430 K and 440 K. These temperatures are higher than the experimental results (Figure 1) due to the so-called size effect: the molecular simulation with small number of molecules provides higher phase transition temperatures due to excessive influence of the periodic boundary condition. 
Figure 5. Snapshots of 8CB-BULK at various temperatures at 1.6 ns. Figure 6 shows the snapshots of 8CB-FSF and 8CB-BULK at 350 K. Though the simulations were performed under completely equal conditions, the difference in the structure clearly appeared: 8CB-FSF was in the crystalline phase and 8CB-BULK was in the N phase. 
Figure 6. Snapshots of the molecular structure of 8CB-FSF and 8CB-BULK at 350 K and 1.6 ns. Figure 7 shows the temperature dependence of the orientational order parameter S for 8CB-FSF and 8CB-BULK. The values of S agree with the phase sequences estimated from the snapshots (Figures 4, 5). The 8CB-FSF system between 300 K and 380 K shows high order parameters corresponding to the crystalline phase, and the system between 380 K and 410 K shows the intermediate order parameters corresponding to the SmA phase. In the case of the bulk, the system between 300 K and 320 K is in the crystalline phase, and the system between 330 K and 340 K is in the SmA phase. It should be noted that the FSF shows the SmA phase in a higher and wider temperature range than the bulk. This result was also observed for an analogue liquid crystal (MHPOBC) by transmission ellipsometry measurement [15]. The origin of the stability of the FSF is the asymmetric intermolecular interaction caused by the existence of the interfaces. For a liquid crystalline molecule near the interface, the inward van der Waals attractive force is dominant over the outward one, because the liquid crystalline molecules in the film have much larger density and molecular weight than the N2 and O2 molecules in the atmosphere. Therefore, the liquid crystalline molecules are shifted inward slightly and their axial molecular motions are suppressed. 
Figure 7. Temperature dependence of the orientational order parameter S of 8CB-FSF and 8CB-BULK at 1.6 ns in the layer structure. Figure 8 shows the temperature dependence of the layer spacing h for 8CB-FSF and 8CB-BULK. The layer spacing was calculated from the average positions of the center of gravity of the molecules in each layer. The h of 8CB-FSF is almost constant (20 Å) in the crystalline phase between 300 K and 370 K, and h gradually decreases to 15 Å in the SmA phase between 380 K and 410 K. In contrast, h in the bulk is independent of the phase and temperature. In the case of SmA phase, h in the FSF is smaller than that in the bulk. This shrinkage was also observed in our transmission ellipsometry measurement [1]. The main origin of the shrinkage is the aforementioned asymmetric intermolecular interaction by the existence of the interface. The decrease in S have little influence on such shrinkage, because the FSF at 390 K shows smaller h than the bulk at 330 K in spite of the fact that these two systems provide almost equal S for instance. 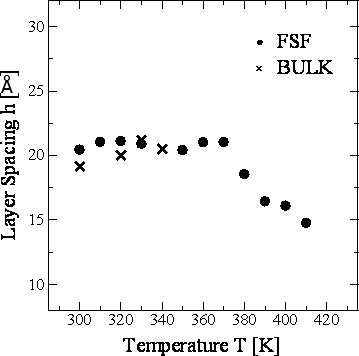
Figure 8. Temperature dependence of the layer spacing h of 8CB-FSF and 8CB-BULK at 1.6 ns in the layer structure. Figure 9 shows the temperature dependence of the film thickness d for 8CB-FSF and 8CB-BULK. The film thickness for the FSF was calculated from the average positions of the outermost atoms of the molecules in the top and bottom layers. In the case of the bulk, this calculation was performed for the same number of smectic layers as the FSF. The d shows similar temperature dependence to h (Figure 8). 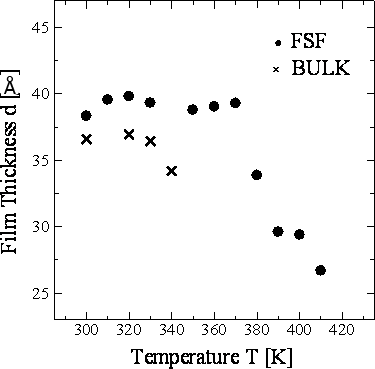
Figure 9. Temperature dependence of the film thickness d of 8CB-FSF and 8CB-BULK at 1.6 ns in the layer structure. Conclusions The free-standing film (FSF) of a liquid crystal 4-octyl-4’-cyanobiphenyl (8CB), which was observed in our previous studies [1-3] for the first time, was reproduced by the molecular dynamics (MD) simulation using the ordinary pairwise atom-atom force parameters without any special phenomenological constraints. This result implies that the free-standing film is stabilized mainly by the van der Waals attractive force between the liquid crystalline molecules, while the precise phase transition mechanism requires further investigation. The simulation allowed preliminary analyses of the transition temperature, the order parameter, the layer spacing and the film thickness. These analyses suggest that the existence of the interface stabilizes the free-standing films and reduces their film thickness. The most significant result, which agrees with the experimental observation, is that the free-standing film shows the SmA phase in a higher and wider temperature range than the bulk. The investigation of the layer spacing and stability is essential for developing application devises using free-standing films, while the experimental analyzing systems have not been developed sufficiently. Further precise simulations together with experimental analysis are expected to elucidate the formation mechanism of the free-standing films. References 1. N. Matsuhashi, Y. Okumoto, M. Kimura and T. Akahane, “Determination of Film Thickness and Anisotropy of the Refractive Indices in 4-octyl-4’-cyanobiphenyl Liquid Crystalline Free-Standing Films”, Jpn. J. Appl. Phys., 41 (2002) 4615-4619. 2. N. Matsuhashi, Y. Okumoto, M. Kimura and T. Akahane, “Transmission Ellipsometry of 4-Octyl-4’-Cyanobiphenyl Liquid-Crystalline Free-Standing Films”, Jpn. J. Appl. Phys., 43 (2004) 2624-2625. 3. N. Matsuhashi, Y. Okumoto, M. Kimura and T. Akahane, “Optical Properties of 4-Octyl-4’-Cyanobiphenyl Liquid-Crystalline Free-Standing Films”, Jpn. J. Appl. Phys., 44 (2005) 582-586. 4. D. J. Cleaver and D. J. Tildesley, “Computer Modeling of the Structure of 4-n-octyl-4’-cyanobiphenyl Adsorbed on Graphite”, Mol. Phys., 81 (1994) 781-799. 5. M. Yoneya and Y. Iwakabe, “Effects of Polymer Surface Structures on Liquid Crystal Alignment Studied with Molecular Dynamics Simulations”, Liq. Cryst., 21 (1996) 817-827. 6. Y. Ouchi, Y. Takanishi, H. Takezoe and A. Fukuda, “Chevron Layer Structure and Paraboic Focal Conics in Smectic A Liquid Crystals”, Jpn. J. Appl. Phys., 28 (1989) 2547-2551. 7. Y. R. Shen, “Studies of Liquid Crystal Monolayers and Films by Optical Second Harmonic Generation”, Liq. Cryst., 5 (1989) 635-643. 8. M. Takeuchi, K. Ishibashi and T. Ishigai, “Development and Application of MASPHYC Computational Material Design System, “Application Package in HPC””, FUJITSU Sci. Tech. J., 33 (1997) 52-61. 9. T. Miyazaki, H. Hayashi and M. Yamashita, “Molecular Dynamics Study on Structure and Stability of Antiferroelectric Smectic Materials”, Ferroelectrics, 245 (2000) 139-146. 10. H. Toriumi, M. Yoshida, M. Mikami, M. Takeuchi and A. Mochizuki, “Computer Simulation of an Antiferroelectric Liquid Crystalline Molecule: The Origin of Bent Structure Formation and the Molecular Packing Property of MHPOBC in Crystalline Phase”, J. Phys. Chem., 100 (1996) 15207-15210. 11. S. L. Mayo, B. D. Olafson and W. A. Goddard, “DREIDING: A Generic Force Field for Molecular Simulations”, J. Phys. Chem., 94 (1990) 8897-8909. 12. W. L. Jorgensen, J. D. Madura and C. J. Swenson, “Optimized Intermolecular Potential Functions for Liquid Hydrocarbons”, J. Am. Chem. Soc., 106 (1984) 6638-6646. 13. S. Nose, “A Unified Formulation of the Constant Temperature Molecular Dynamics Methods”, Mol. Phys., 52 (1984) 255-268. 14. M. Parrinello and A. Rahman, “Crystal Structure and Pair Potentials: A Molecular-dynamics Study”, Phys. Rev. Lett., 45 (1980) 1196-1199. 15. Y. Okumoto, M. Kimura, T. Akahane and N. Matsuhashi, “Investigation of Layer Structure of MHPOBC Free-Standing Film by Transmission Ellipsometry”, Mol. Cryst. Liq. Cryst., 365 (2001) 835-844. 16. A. J. McDonald and S. Hanna, “Atomistic Computer Simulations of Terraced Wetting of Model 8CB Molecules at Crystal Surfaces”, Mol. Cryst. Liq. Cryst., 413 (2004) 135-144. 17. M. I. Caper and E. Cebe, “Rotational Viscosity in Liquid Crystals: A Molecular Dynamics Study”, Chem. Phys. Lett., 407 (2005) 454-459. 18. Y. Lansac, M. A. Glaser and N. A. Clark, “Microscopic Structure and Dynamics of a Partial Bilayer Smectic Liquid Crystal”, Phys. Rev. E, 64 (2001) 051703. 19. M. R. Wilson and M. P. Allen, “Computer Simulations of Mesogenic Molecules Using Realistic Atom-Atom Potentials”, Mol. Cryst. Liq. Cryst., 198 (1991) 465-477. 20. I. Ono and S. Kondo, “Orientational Ordering and Molecular Motion of 4’-pentyloxy-4-cyanobiphenyl (5OCB) by Molecular Dynamics Simulation”, Mol. Cryst. Liq. Cryst. Lett., 8(4) (1991) 69-74. Contact Details |