Investigating the Impact of Particle Characteristics on Suspension Rheology

Many products are dispersions or suspensions of particles in a liquid medium. Examples range from ceramics, adhesives, inks and paints through to drinks, foods, medicines and personal care products. The physical properties of the dispersed particles in systems such as particle size and its distribution, electric charge (zeta potential), concentration and particle shape can have a strong impact on the overall (bulk) rheological properties of a suspension, which in turn, dictates product behavior and functionality. Understanding these interactions is important for achieving desirable product performance, whether it is a stable medicine or paint, a visually appealing drink or shower gel, or workable cement.

This article analyzes the impact of particle properties on suspension viscosity, and in general, on rheological behavior. It discusses how particle size, particle shape, and zeta potential affect important aspects of suspension performance such as stability and viscosity, and how such properties can be used to customize this behavior.

Understanding the Effect of Particle Concentration

Albert Einstein, in his early career days, investigated and described the flow field around a single hard sphere in a liquid ^{[1, 2]}. He concluded that single particles enhanced the viscosity of a liquid as a simple function of their phase volume, according to the formula.

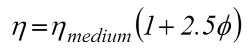
where
η is viscosity of the suspension
η_medium is the viscosity of the medium
Φ is the volume fraction of solids in the suspension

Einstein's findings are of great value for describing systems containing very low particle concentrations. However, in many industrial suspensions, particle loadings are relatively high, and particles with a greater proximity to one another. As a result of this, there is a far more inhibited flow field giving rise to higher suspension viscosities and greater sensitivity to incremental changes in particle concentration. Many semi-empirical models have been developed to take into account this 'crowding' effect; perhaps, the most popular is the one developed by Irvin Krieger and Thomas Dougherty ^[3-5].

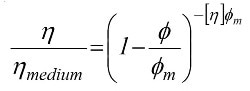
where
Φ_m is the maximum vol. fraction of solids in the suspension
[η] is the intrinsic viscosity (2.5 for spheres)

The Krieger and Dougherty equation defines the relationship between particle loading or concentration and viscosity in this regime of higher particle concentrations, and in addition to the parameters described in Einstein's equation, includes an extra parameter, the maximum packing fraction, Φ_m. This is the maximum volume of particles that can be added to a suspension prior to the system getting 'jammed up' and viscosity becoming infinite.

Figure 1 illustrates how the viscosity of a suspension gets altered when the volume fraction of particles is increased, relative to the maximum volume fraction. At low volume fractions, where Φ/Φ_m is less than 0.1, there is space for the particles to move freely, a situation closer than Einstein’s. The suspension demonstrates the Newtonian response of the continuous phase which means that viscosity does not depend on shear rate. However, the fluid has a higher viscosity since it has to circumvent the dispersed particles.

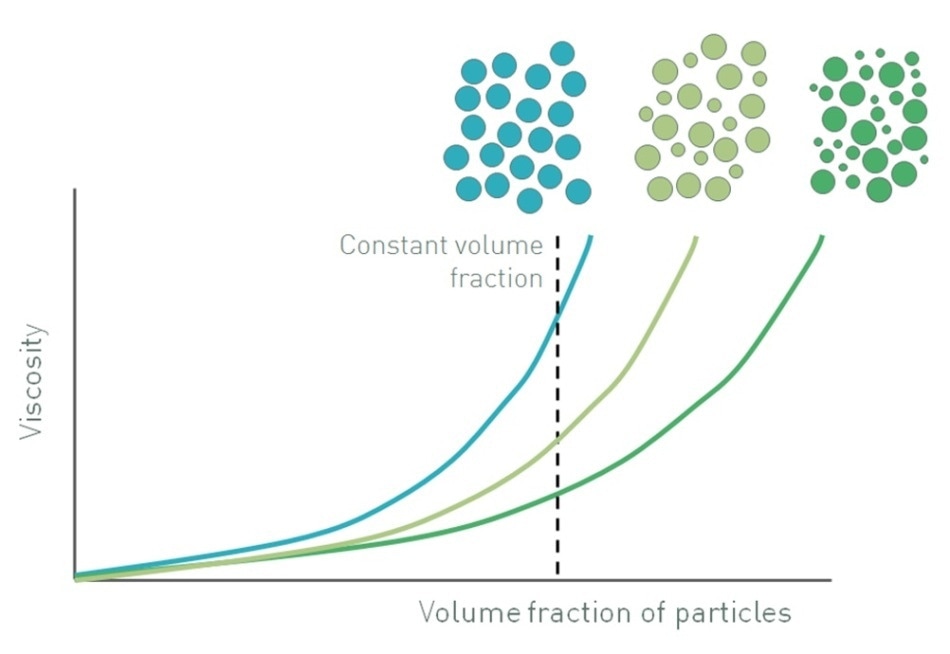
Figure 1. Increasing the volume fraction of particles in a suspension increases viscosity and also influences whether a suspension will exhibit Newtonian or non-Newtonian behavior

When the volume fraction increases, typically in the range of 0.1-0.5, particle-particle interactions become significant. These interactions hinder the freedom of movement of the particles, and also affect fluid flow around adjacent particles, resulting in increased viscosity. However, when shear rate is increased, the particle-particle interactions are broken down since the strength of the interactions is relatively low. This effect is compounded by the impact of Brownian motion, particularly in suspensions consisting of fine particles, which exhibit relatively high Brownian stresses. Brownian motion acts opposite to an applied shear stress, and seeks to maintain randomized particle movement. This effect is nullified at higher stresses when particles are able to rearrange themselves into a more efficient packing structure by forming strings and rafts ^{[4, 5]}. Both mechanisms bring about non-Newtonian, shear thinning behavior such that viscosity no longer depends on shear rate or shear stress (Newtonian) but decreases when shear is increased.

At even higher particle loading, when Φ/Φ_m becomes more than 0.5 or 0.6, there is not much space for the particles to move with the result that the flow field around particles is much more complex. In this situation, the particles are interacting with one another and are also physically restricting their mutual motion with the fluid acting as a lubricant. When shear increases, this restriction of movement increases, and the suspension shows shear thickening behavior in which viscosity increases with shear rate because of formation of particle clusters or particle jamming. The actual figures of Φ/Φ_m marking the transition from Newtonian to shear thinning and then to shear thickening behavior are system-specific but those included in this article offer a good guideline in most cases. The shear rate or shear stress at which shear thickening occurs is also system-dependent ^[5].

Optimizing Particle Properties – The Effect of Concentration, Size and Shape

Effect of Volume Fraction

If there is no change in volume fraction, then reduction in particle size results in an increase in the number of particles present. This particularly holds good for submicron-sized particles. In the case of these particles, the effective hydrodynamic size may be significantly increased by any surface charge, hydration or adsorption layers surrounding each core particle. This results in a higher effective volume fraction for a given particle loading, thus increasing the viscosity of the suspension. This effect is considerably reduced for larger particles that are less in number.

Data for latex particles in a pressure-sensitive adhesive illustrating this effect is shown in Figure 2. Since inter-particle (colloidal) interactions are dominant at low shear rates, the effect is more noticeable in this range with smaller particles showing higher viscosities because of their higher effective volume. At high shear rates, the inter-particle forces get broken down and hydrodynamic forces become dominant. Consequently, the effective volume fraction is less dependent on particle size and viscosity values converge.

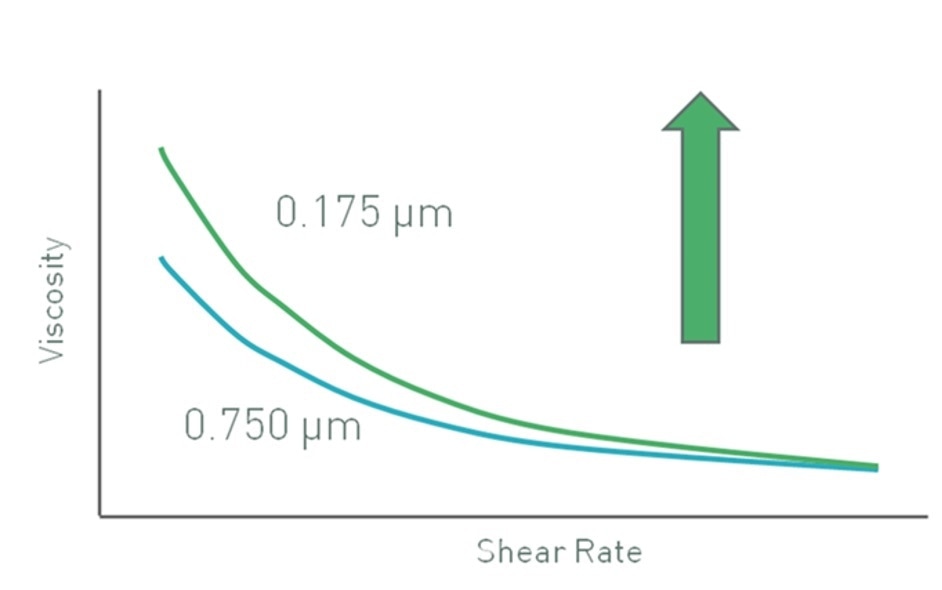
Figure 2. Decreasing particle size may lead to an increase in low shear viscosity, for a constant volume fraction of particles, if colloidal interactions are significant

Brownian motion is also an important factor as this is opposed to any applied shear stress and is particle size-dependent. Therefore, shear thinning begins at higher shear rates or stresses for smaller-sized particles.

Effect of Particle Size Distribution

Polydispersity is the range or span of the particle size distribution. A wide-spanned particle size distribution consists of dissimilarly sized particles – small and large – which can pack more efficiently as compared to a collection of monodisperse particles, thus providing more free room and allowing easy movement of an equivalent volume of particles, hence reducing viscosity. In terms of the Krieger-Dougherty equation, this increase in polydispersity results in an increase in the maximum volume fraction, thus reducing viscosity. Conversely, narrowing of the particle size distribution increases viscosity, a change often accompanied by increased stability.

The effects of particle size and polydispersity can sometimes be competing. Hence, particle size and its distribution can be jointly employed to control viscosity. Referring to the earlier example of using either 175 nm particles or 750 nm particles (Figure 2), a bimodal distribution of these two particles results in a minimum viscosity (Figure 3). For a specific volume fraction, suspension viscosity with only 750 nm particles is lower than that with 175 nm since the use of finer particles enhances the effective volume fraction. However, viscosity is increased because of the inclusion of a relatively small fraction of 175 nm particles to make a binary mixture. The influence of these finer particles on packing behavior, which reduces viscosity, more than balances the increased viscosity because of a greater number of particle-particle interactions.

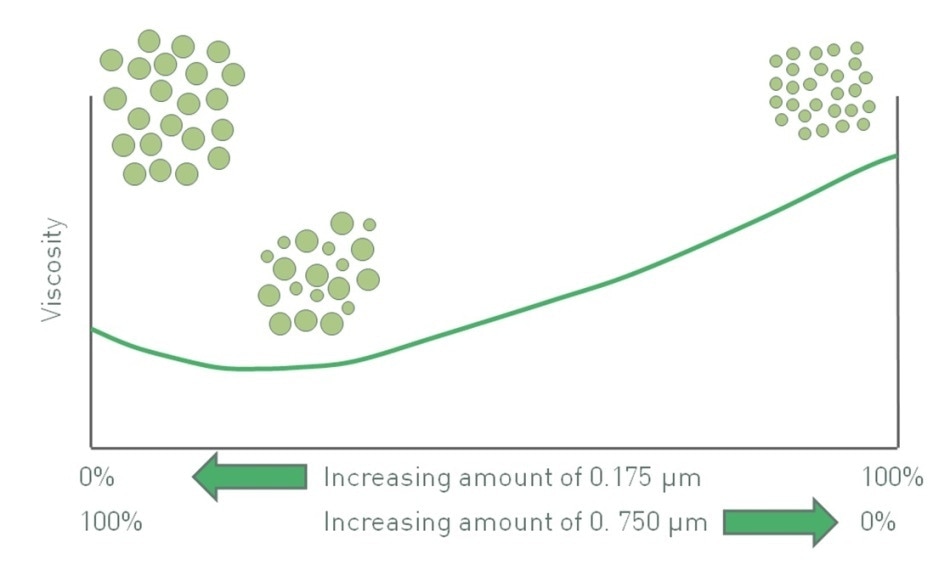
Figure 3. The impact of polydispersity and particle size can produce competing effects and in the system above produces a minimum viscosity value

Effect of Particle Shape

Convexity is a measure of the regularity or sharpness of the perimeter of a particle, a descriptor of particle shape. Figure 4 shows that particles having low convexity have a convoluted outline, increasing the possibility of mechanical resistance to flow in a suspension. Moreover, relative to equivalently-sized smooth particles, particles having low convexity may exhibit a high specific surface area, thus increasing the number of particle-particle interactions and any associated chemical interactions. The two effects are more pronounced at high solids loadings. Even at lower volume fractions, higher particle roughness or shape irregularity can lead to increased viscosity as the liquid flow is deviated around them. Considering these effects, the viscosity of a suspension can often be decreased by using smoother, more regular-shaped particles. However, any impact is usually more pronounced at high volume fractions and low shear rates.

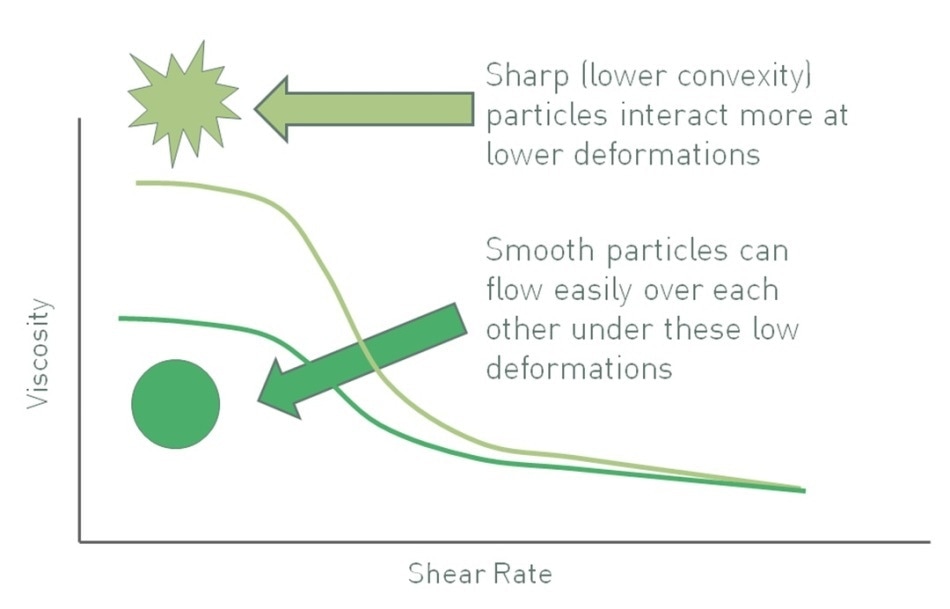
Figure 4. Sharper particles, those with lower convexity, give rise to suspensions with higher viscosity, all other factors being equal

Elongated particles generate a different suspension viscosity profile as compared to spherical particles. In spherical particles, particle-particle interactions typically break down when shear increases, giving rise to shear thinning behavior. Elongated particles randomly orient at low shear and occupy larger volumes, but at high shear, will tend to orient along the direction of flow to result in more efficient packing. Consequently, suspensions with elongated particles also shear thin, but in a far more pronounced manner than those consisting of spherical particles. In terms of the Krieger-Dougherty relationship, particle irregularity increases the intrinsic viscosity [η] relative to that of a sphere and decreases the maximum packing fraction to provide a higher low shear viscosity.

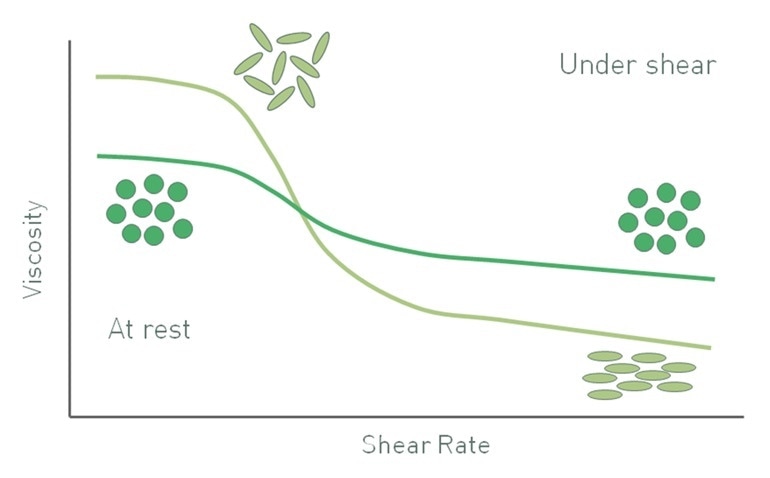
Figure 5. As a result of orientation at high shear rates the viscosity of suspensions with elongated particles has a different profile from that of a suspension containing spherical particles of equivalent size

Effect of Zeta Potential

The earlier analysis of how particle size and particle shape affect viscosity has shown that these physical characteristics impact the easy movement of particles, relative to one another within a suspension. Another parameter influencing particle movement, and hence stability and viscosity, is the electrical charge on particles within a system. One of the ways to measure this charge is to quantify zeta potential.

Zeta potential refers to the amount of the electrostatic attraction or repulsion in a system. It is a measure of particle charge at the edge of the slipping plane between the particle and associated double layer, and the surrounding solvent (Figure 6). Zeta potential is the charge at the edge of the particle’s ‘sphere of influence’ and not the charge on the surface of the particle, makes it highly relevant to suspension behavior. If a suspension has a high negative or positive zeta potential, then the particles within it are likely to repel each other. Low zeta potential values increase the possibility of agglomeration or flocculation, the joining together of discrete particles.

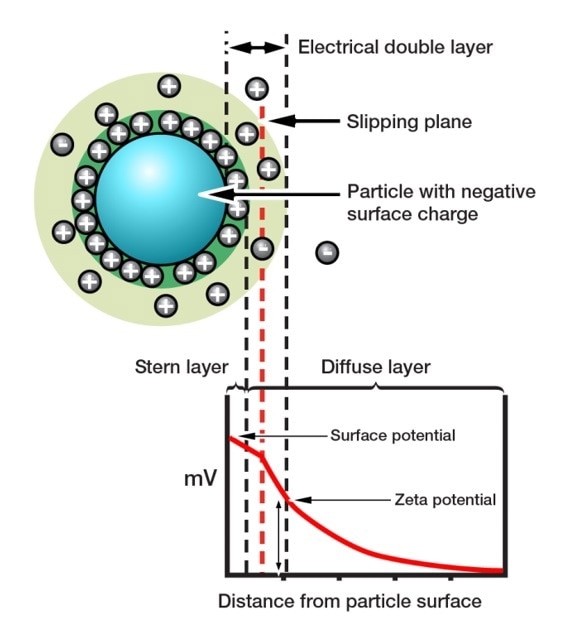
Figure 6. Zeta potential influences whether particles will repel or attract when held in suspension

In colloidal systems, particles have a tendency to move under Brownian motion with the influence of gravity being low since particle mass is small. In such a case, when the zeta potential is increased, it causes particles to repel one another, restricting the movement and increasing viscosity, particularly at low shear rates (Figure 7). At low shear rates, the particles have a larger effective hydrodynamic volume because of their charge. A zeta potential of considerable magnitude, around ±30 mV, will maintain particle separation. In these systems, if the particles agglomerate and grow in mass, gravitational forces only become large enough to cause sedimentation. Therefore, separation of particles ensures stability ^[6].

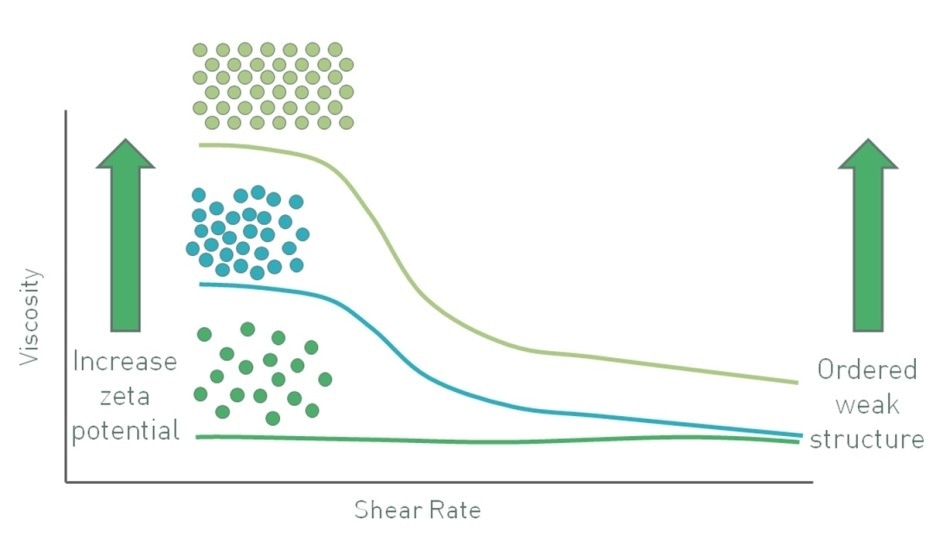
Figure 7. In a colloidal suspension with sub-micron particles increasing zeta potential increases viscosity at low shear stress through an increase in the particles effective phase volume

In a suspension containing larger particles, control of zeta potential delivers a quite different effect. For particles having substantial mass, gravitational forces are enough to cause sedimentation. In such cases, a stable suspension cannot be generated by inducing a high zeta potential in order to maintain the particles as discrete entities. However, the converse works. In certain systems, decreasing the zeta potential causes partial agglomeration of the particles, thus forming a networked gel that can contribute appreciable viscosity to a suspension, and generate an apparent yield stress, as shown in Figure 8 ^[6].

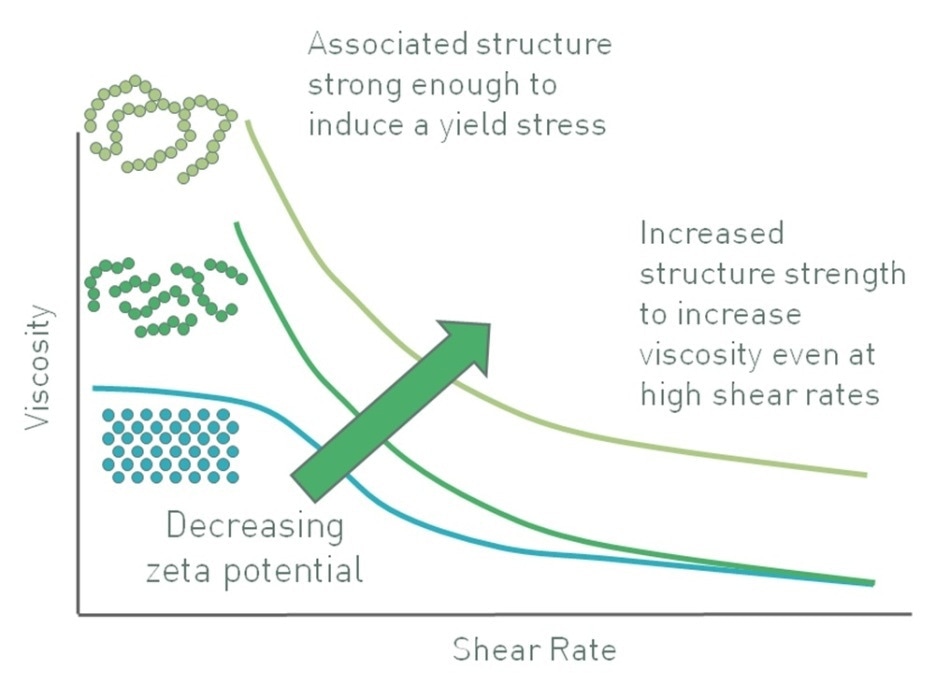
Figure 8. Decreasing zeta potential can induce a flocculated particle gel with an apparent yield stress that enhances stability

Tools for Characterizing Suspensions

Several strategies can be adopted to refine rheological properties so as to satisfy performance targets for a specific suspension. However, such formulation optimization has to be based on analytical data. Dynamic light scattering (DLS) and laser diffraction are proven techniques for determining particle size distributions centered in the sub-micron and micron ranges, respectively. Electrophoretic light scattering (ELS) is a technique that is complementary to DLS and often integrated in dynamic light scattering systems. It can be used to measure zeta potential, while automated imaging provides rapid, statistically-relevant particle shape analysis.

Rotational rheometers are perhaps the most versatile rheological tools available for making rheological measurements. The rheometers can be configured for different rheological methods to probe the structure and performance of suspensions. Test types range from producing viscosity flow curves over many decades of shear rate and shear stress, through to measurements of thixotropy, yield stress and viscoelasticity.

Capillary rheometry is employed for measuring viscosity profiles of slurries and suspensions consisting of relatively large particles, at high particle loadings. Industrial examples include ceramic slurries, powder injection molding, foodstuffs, coatings, and inks. Capillary rheometers can apply very high force, which enables the study of behavior at much higher shear rates than is possible with rotational rheometers, such as those associated with injection and extrusion.

References

1. Einstein A (1906), Eine neue Bestimmung der Molek ¨ uldimensionen. Ann Physik. 19 289-306.

2. Einstein A (1911), Berichtigung zu meiner Arbeit: "Eine neue Bestimmung der Mole¨k uldimensionen." Ann Physik. 34 591-2.

3. Krieger IM; Dougherty TJ, A mechanism of non-Newtonian flow in suspensions of rigid spheres. Trans Soc Rheol. 3 (1959), 137

4. Barnes HA, Hutton JF and Walters K (1989), An Introduction to Rheology

5. Mewis J, Wagner NJ (2012), Colloidal Suspension Rheology

6. Suspension Stability Suspension Stability; Why Particle Size, Zeta Potential and Rheology are Important – Malvern Panalytical application note http://www.malvern.com/en/support/resource-center/application-notes/AN101130SuspensionStability.aspx

This information has been sourced, reviewed and adapted from materials provided by Malvern Panalytical.

For more information on this source, please visit Malvern Panalytical.