An idealized one-degree-freedom isolator, based on a simple harmonic oscillator, is shown in Figure 1. The isolator consists of three parts. The first is the isolated mass (M), which represents the payload being isolated and is depicted as a single block of mass devoid of internal resonances.
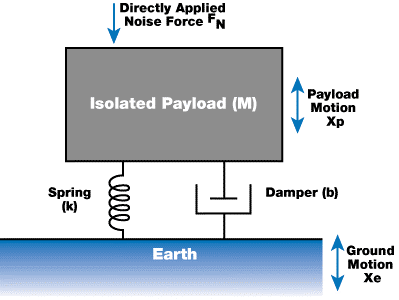
Figure 1
The second component is the spring (k), which supports the payload and generates a force on the payload which is expressed as:
| Force = k x (Xe – Xp) |
[1] |
where Xp and Xe denote the (dynamic) position of the payload and the earth, respectively.
The damper (b) is third component, which is schematically shown as a dashpot. The damper absorbs any kinetic energy of the payload, converts it into heat, and consequently brings the system to rest. This is carried out by generating a force on the payload which is opposite and proportional to its velocity relative to the earth:
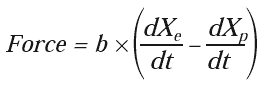 |
[2] |
Xe exists in the two equations, which shows that the earth’s vibration is transmitted as a force to the payload by the damper and the spring. Instead of using the three parameters ((M), (k), and (b)) to describe a system, another set of parameters is commonly used that relate more easily to the observed quantities of the mass-spring system. The first of the new set is the natural resonant frequency ω0:
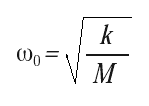 |
[3] |
The natural resonant frequency describes the free oscillation frequency for the system when there is no damping (b = 0) in radians/second. The frequency, expressed in cycles per second, or Hertz (Hz), denotes this angular frequency divided by 2π. Of the two common parameters is used to describethe damping effect in a system: the quality factor Q or the damping ratioζ:
 |
[4] |
The transmissibility for this idealized system is expressed as:
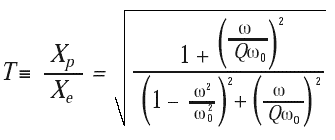 |
[5] |
The transmissibility of the system versus the frequency ratio ω/ω0 for a range of values of the quality factor Q is plotted in Figure 2. The plotted Q values vary from 0.5 to 100. The case when Q is 0.5 is referred as critical damping and denotes the level of damping where the system does not overshoot the equilibrium position if it is displaced and released.
The damping ratio ζ is a fraction of the system’s damping to critical damping. Q can be used instead of ζ because T ≃ Q at ω = ω0, for Qs values greater than 2. Figure 2 shows several features that characterize the transmissibility of a system.
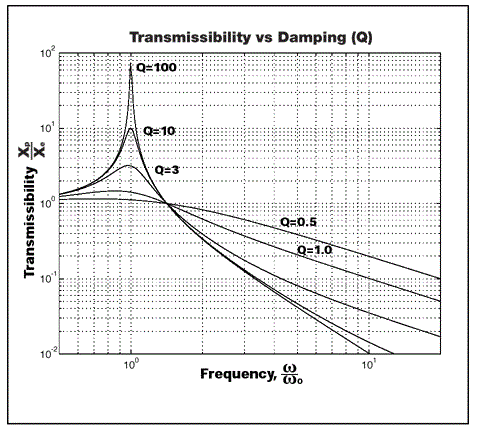
Figure 2
- The transmissibility for the system is ≃ 1 in the region ω < < ω0, meaning the payload tracks the earth’s motion and isolation is not provided
- The transmissibility is greater than 1 in the region ω ≃ ω0, and the ground motion is amplified by the spring/damper isolator by a factor roughly equal to Q
- The transmissibility becomes proportional to (ω0/ω)2 when ω becomes greater than ω0, and this the region where the isolator proves to be beneficial
- The system provides the best isolation in the region ω > > ω0, with the smallest damping level. However, the level of isolation is compromised with increasing damping and therefore, a tradeoff will always be there between providing isolation in region ω > > ω0 versus ω ≃ ω0.
The amplitude of motion transmitted to the payload by the forces that are directly applied to it takes a slightly different form than that expressed in equation 7. This transfer function is expressed in displacement per unit force, so it should not be confused with the term transmissibility.
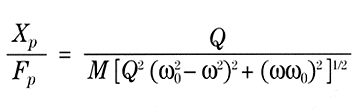 |
[6] |
Figure 3a plots this function versus frequency. In contrast to Figure 2, when Q factor is lowered, the payload’s response at all frequencies, including the region ω > > ω0, is reduced.
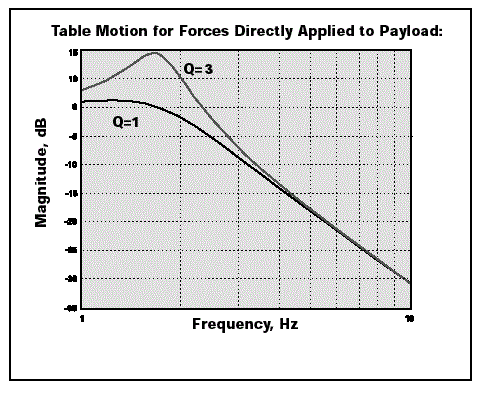
Figure 3a
TMC’s MaxDamp® isolators take advantage of this for applications where the main disturbances are produced on the isolated payload. Figure 3b demonstrates the payload’s time-domain response corresponding to the curves illustrated in Figure 3a. Figure 3b also shows the system decay when disturbed. The envelope for the decay is exp (-ω0t/2Q).
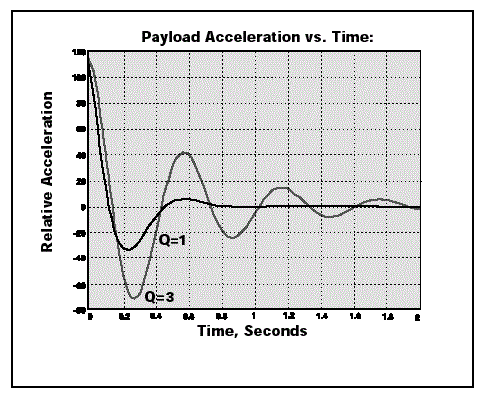
Figure 3b
Significant differences exist between real systems and the simple model shown in Figure 1, and the most important of which is that the real systems possess six degrees-of-freedom (DOF) of motion. The DOFs are not independent but strongly couple in most systems.
For instance, “horizontal transfer functions” typically shoe two resonant peaks because a payload’s horizontal motions are driven by tilt motions and vice-versa.
Pneumatic Isolators
A simplified pneumatic isolator is shown in Figure 4. The isolator works according to the pressure in the volume (V) acting on the area of a piston (A) to secure the load against the gravitational force.
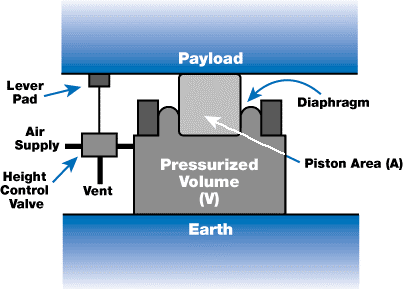
Figure 4
A seal is formed between the piston and the air tank by a reinforced rolling rubber diaphragm. The isolator pressure is regulated by a height control valve which detects the payload’s height and inflates the isolator until the payload is “floating.” Pneumatic isolators provide many benefits. The payload’s resonant frequency on such a mounts is approximately:
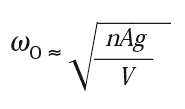 |
[7] |
Here, n is the gas constant for air and equal to 1.4, and g is acceleration of gravity (386 in/s2 or 9.8 m/s2). Unlike steel coil springs, the resonant frequency is nearly independent the payload’s mass, and the height control valve ensures that the payload is brought back to the same operating height.* Gas springs are very lightweight, and do not have internal spring resonances that can degrade the performance of the isolator.
The isolator’s load capacity is set by the piston area and the maximum tolerable pressure of the diaphragm and is the product of these two numbers. The load capacity is usually rated at 80 psi of pressure. This can enable a 4-in. piston to support a 1,000-lb load, for example. Although the simple isolator illustrated in Figure 4 will work, it has very minimal horizontal isolation and damping.
*Equation 7 assumes the isolator’s pressure is high compared with atmospheric pressure. Lightly loaded isolators will exhibit a slightly higher resonant frequency.

This information has been sourced, reviewed and adapted from materials provided by TMC.
For more information on this source, please visit TMC.