The design and manufacturing of plastic based engineering components, essentially need the measurements of their viscoelastic properties. In the experiment performed the iNano nanoindentation system from Nanomechanics, Inc. was used to quantify time-dependent deformation in polycarbonate, a thermoplastic polymer. A Berkovich indenter was used in a constant-load-hold technique to measure indentation strain rate as a function of mean contact pressure. The results were found to be extremely repeatable. The testing technique was nondestructive and can be used for both material characterization and quality control.
Materials and Methods
The Polycarbonate used for testing was obtained from Goodfellow Corp., USA. Time dependent deformation is tested using the constant load and hold technique. The sample was loaded as an exponential function of time to a target load (e.g., Fig. 1). Following the loading segment, the instrument held the applied load, P, on the sample constant for a set period of time over which the indentation depth, h, was monitored (e.g., Fig. 2). The sample was completely unloaded following the end of the hold. Each indentation test time was ~75s, and a total of 9 indentations were performed.
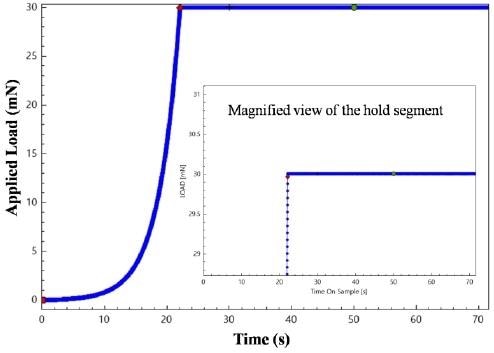
Figure 1. Load time history for the creep testing. Initially, the sample is loaded at a constant indentation strain rate followed by a hold segment where the creep rates are measured.
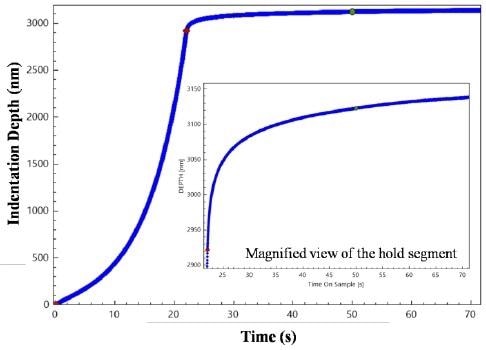
Figure 2. Indent depth time history resulting from the loading. Depth changes with time during the load hold segment are directly related to creep deformation.
The calculations were based on the given equations where Indentation strain-rate, was calculated from the indentation depth, h, and time, t, given in Eq. (1). Assuming that the contact depth is equivalent to the indentation depth, the contact area, A, was calculated according to Eq. (2) for a Berkovich indenter. The mean contact pressure, H, was calculated by Eq. (3).
Results and Discussion
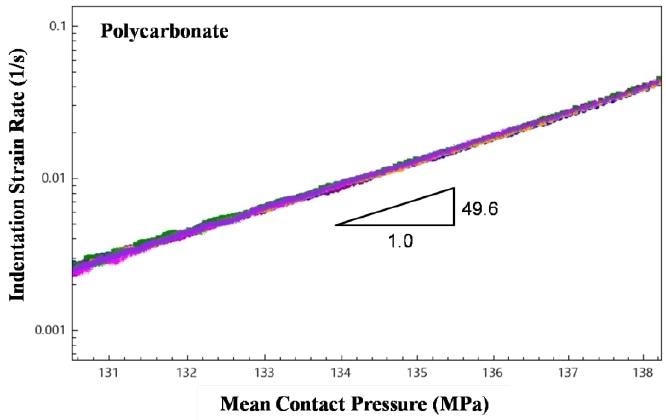
Figure 3. Indentation strain rate plotted as a function of mean contact pressure (log-log scale) for all 9 tests. The slope of the data determines the creep behavior of the material.
Indentation strain-rate as a function of mean contact pressure is plotted in Fig. 3. A change in mean contact pressure of 7 MPa caused a change in indentation strain-rate of nearly two orders of magnitude. This time-dependent behavior was found consistent with conventional viscoelastic theory, i.e., larger applied pressures result in higher strain-rates. For material characterization purposes, the data in Fig. 3 can be fit to a power-law behavior to give the change in strain-rate with respect to change in applied pressure. The resulting slope for this particular grade of polycarbonate was found to be 49.6 as shown in Fig. 3.
Conclusions
Using the iNano nanoindentation system from Nanomechanics gives the capability to rapidly and accurately characterize time-dependent behavior in polymers and other viscoelastic plastics. In this work, a constant-load-hold test with a Berkovich indenter revealed a positive and repeatable relationship between strain rate and contact pressure. The quick and accurate testing done simply and with precision by the iNano make it extremely well suited for quality control applications in industry.
References
[1] C. Su, E.G. Herbert, S. Sohn, J. A. LaManna, W. C. Oliver, and G. M. Pharr, JMPS, 2013.
[2] E. G. Herbert, K. E. Johanns, R. Singleton, and G. M. Pharr, JMR, 2013.

This information has been sourced, reviewed and adapted from materials provided by Nanomechanics, Inc., a KLA-Tencor company.
For more information on this source, please visit KLA.