Size and shape are measures that greatly determine particulate behavior such as flowability, compaction, and mixing. Spherical particles are adequately characterized by size-only techniques. However, irregular particles require additional shape measurements to best characterize them and understand how your particles will perform.
Highly irregular shaped particles are hard to characterize, but for raw material particles in manufacturing, just knowing particle size is not enough. To truly understand particle behavior, it is required to measure more shape parameters and have tools that use these shape parameters to predict performance. The irregularity of particles and their use in final products will indicate the shape measurements needed to properly gain a better understanding and control to optimize the final product.
Dynamic image analysis is becoming more popular as a complementary analysis method because end users are beginning to understand the importance of large amounts of data for a large sample population. The first and most basic report of any particle size and shape analysis comes in the form of a statistical histogram. They are an excellent way to view channelized data in number weighted as well as volume weighted distributions.
Distribution Histograms
To illustrate the statistical results from sample analysis, results are divided into small classes or “bins,” and the number of particles in each size bin is reported. Size information can be displayed in volume, number, and surface-area weighted histograms, each offering valuable information about the analyzed sample. Because dynamic image analysis is a number-based instrument, which means that each particle is identified and measured individually, the statistical histograms are very exact in each size bin. For example, in dynamic imaging systems users can easily view exactly how many particles are allocated in each of the size bins. Of course, since it is an imaging system, the user can also see the individual particle thumbnail images that offer some objective evidence of what is being measured. Size data is usually depicted graphically on a log scale axis. Size and shape histograms are commonly used to compare differences in lots of samples.
Below are particle size histograms. These three histograms are of the same sample. Users should always view, had a very minimum, the number weighted distribution as well as the volume weighted distribution. Number weighted distribution is important for the user to view very fine particles. Very fine particles can impact a process where filtration can be clogged easily. In some cases, the presence of fine particles is important because they help lubricate the movement and flowability of particles. Therefore, there are different cases where fine particle presence can be a good thing or a bad thing. This is why number-weighted distributions should always be reviewed. Below you will also find a volume weighted statistical histogram. Volume weighted distributions are important to monitor large particle presence. Again, like fine particles, the presence of large particles may be wanted or undesirable. This is why viewing volume-weighted statistical distributions is also important. Surface area weighted distributions are sometimes used to gain an understanding of how much surface area a particle may have. However, there must be well understood that this is merely a calculation and does not take into consideration porosity. If your sample requires a more in depth understanding of surface area and porosity, it is recommended to look at equipment that can measure the specific properties. The last display of sieve equivalency is typically used for customers that have been using manual sieve measurements and are interested in converting to an automated method.
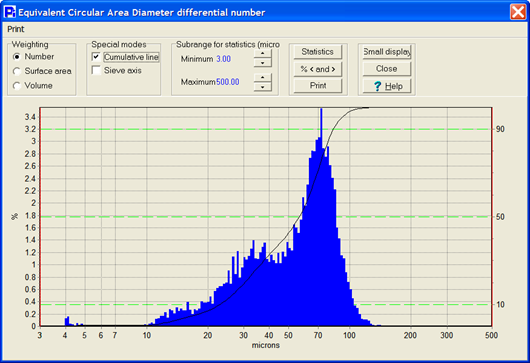
Figure 1 A Number-weighted size histogram will show presence and quantity of fine particles in a sample.
Image Credit: Vision Analytical Inc.
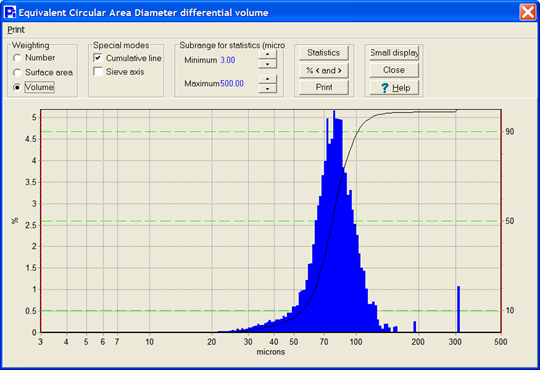
Figure 2 A Volume-weighted size histogram will show presence and quantity of Large particles in a sample.
Image Credit: Vision Analytical Inc.
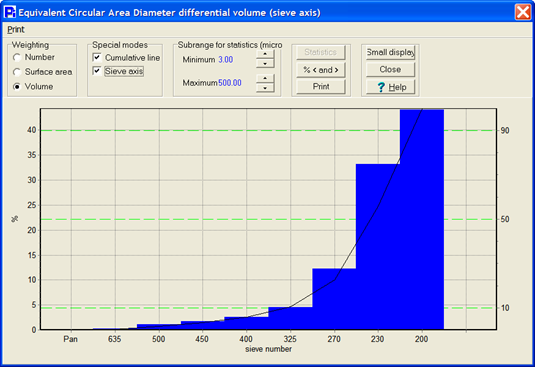
Figure 3 Sieve Correlationd size histogram typically used to compare to older Sieving techniques.
Image Credit: Vision Analytical Inc.
In some cases, shape measurements are size-independent. In such cases, these fraction measures range from a value of zero to one. The following graph is a histogram showing a distribution of smoothness which is a measure of the irregularity in the perimeter of a particle. In this case the value of zero “0” would represent a very un-smooth particle and the value of one “1” would represent a very smooth particle. There are many other fraction measurements for shape such as circularity, opacity, or aspect ratio. All of these are reported on a linear scale. Each bin reports its recorded quantity of particles
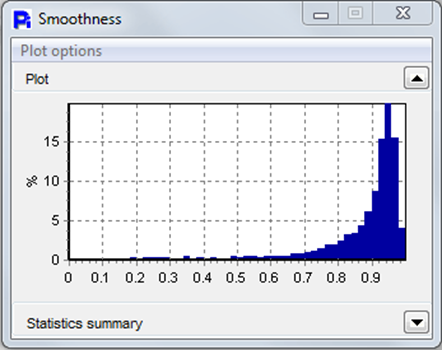
Image Credit: Vision Analytical Inc.
As discussed above, the reporting of number and volume-weighted distrubutions are very informative. Volume-weighted histograms will emphasize the presence of larger particles over the smaller ones, given the more significant volume larger particles have compared to a higher number of smaller ones. Volume-weighted histograms are helpful to identify small amounts of agglomerates in samples. Number-weighted histograms are helpful to identify large quantities of fine particles in samples, resulting in clogging or filtration issues. Of course, using dynamic image analysis, objective evidence of these particles are given in the form of thumbnail images of every measured particle:
The following chart explains why one sample can have different number-weighted and volume-weighted histograms. This also shows the benefit of always studying both weighted statistics and using both to compare and contrast. The number and volume weighting can offer value in observing small quantities of agglomerates (larger particles) by reporting by volume and a higher number of fines (smaller particles) reporting by number.
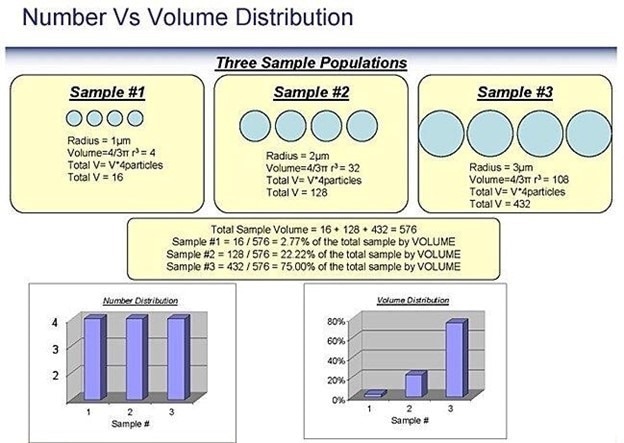
Image Credit: Vision Analytical Inc.
More on Statistics
A typical statistical result not only gives the graphical histogram, but also will report a large amount of data. Below is a sample of a size-based histogram and associated data.
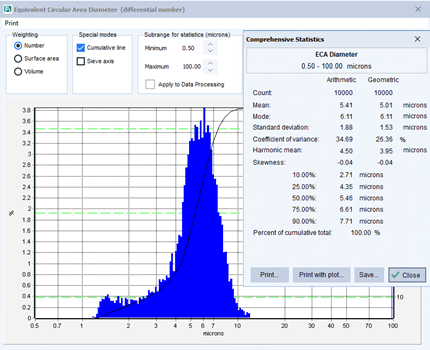
Image Credit: Vision Analytical Inc.
A typical size distribution is characterized by different values. One of the most common being the mean size. A mean value allows some information of the particle size but does not issue any indication about the shape of the distribution or how broad or narrow it is. The number or arithmetic mean is purely the average value. It is frequently denoted as D1,0. Other means take into account volume weighting and area.
Assuming sphericity of particles, the generic definition of a weighted Dp,q mean diameter is
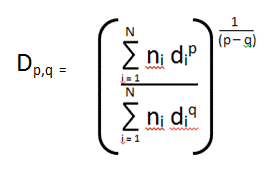
Image Credit: Vision Analytical Inc.
Definition of Dp,q means
The diameter means that are most often of use in characterizing a particle sample are:
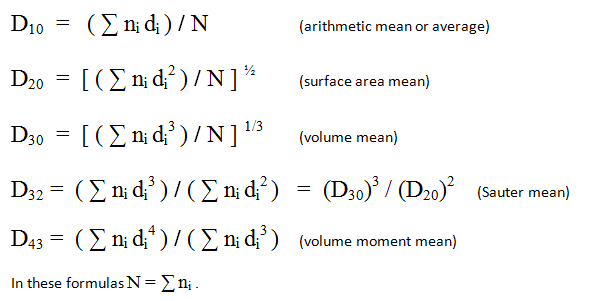
Image Credit: Vision Analytical Inc.
In these definitions, ni is the count in size bin number i, and di is the representative diameter of that size bin. The sums are over all particles, and N is the particle count total.
Descriptions of these means in words are as follows:
Arithmetic mean diameter, D[1,0] : the average of the diameters of all the particles in the sample.
Surface mean diameter, D[2,0] : the diameter of a particle whose surface area, if multiplied by the total number of droplets, will equal the total surface area of the sample.
Volume mean diameter, D[3,0] : the diameter of a particle whose volume, if multiplied by the total number of particles, will equate all of the sample’s volume.
Surface moment mean diameter, D[3,2] (“Sauter mean”): the diameter of a particle whose ratio of volume to surface area is the same as that of the complete sample. Mathematically, if V is the total volume and A is the total surface area of the sample, D3,2 = 6 * (V / A).
Volume moment mean diameter, D[4,3]. This value is an indicator weighted on the volume of particles. This is the mean value that is most commonly used by Laser Diffraction instrumentation..
The Mode is the most frequent size present.
The Harmonic mean is N / Σ (ni / di)
Geometric Means
Geometric means reflect the visual weighting of a log-size axis. The geometric mean diameter will appear as the center of a distribution on a log scale, while the usual arithmetic mean may sit a lot lower on the size scale (as smaller sizes are a lot more numerous than larger sizes).
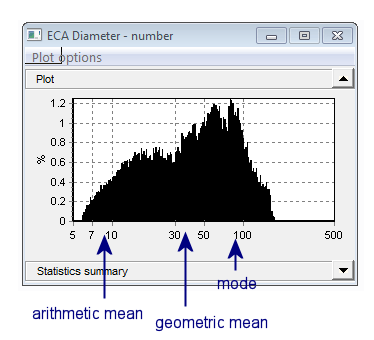
Image Credit: Vision Analytical Inc.
To compute the geometric mean, use the logs of the x-axis values ( log (di) in place of di ) :
The Geometric mean is Σ [ni log(di)] / N
With the use of the same manner, the geometric versions of the other means and standard deviation may be calculated.
Measures of Spread
Standard deviation measures how wide the distribution is:
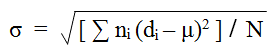
Image Credit: Vision Analytical Inc.
where μ = mean diameter (D10). It has units of microns (for a size distribution).
The Coefficient of Variance is the ratio of the standard deviation to the mean: CV = σ / μ . To express as a percent multiply by 100. Being a ratio, this statistic does not have units.
Percentiles
Percentiles are a way of conducting size information as one or more numbers. The Median size splits the particles into two parts containing equal counts. Strictly speaking, this is the Number Median. It is also known as the 50th or the 50% percentile.
The 10th percentile defines the size with the property that 10% of the particle count is less than that size. Any other percentile can be defined similarly. Commonly, three percentiles (10%, 50% and 90%) are used as a characterization that is uncomplicated but provides additional information to a single mean. Additional percentiles are available and customizable in the Insight software to meet the needs of any specific industry requirement.
The Volume Median, or 50th percentile by volume, splits the volume of the sample into two equal pieces. The two classes will hold equal volume but not an equal count of particles. Other volume percentiles are defined similarly; as an example, the 25th volume percentile is the size such that particles smaller than that size are representative of a quarter of the volume.
Other Characterizations
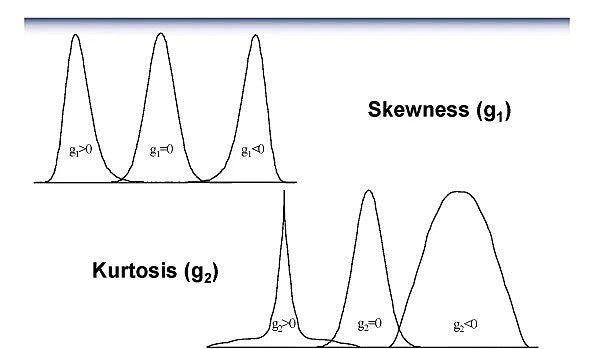
Image Credit: Vision Analytical Inc.
Skewness is an indicator of how asymmetrical the shape of the distribution is, about the center. A positive value will mean there are further counts on the right side of center, normally in the appearance of a tail. A negative value will mean it tails to the left.
Skewness = Σ ni (di – μ)3 / (σ3 N) (σ = std. dev., μ = mean)
Kurtosis is an indicator of how much the shape differs from the typical bell curve in a vertical sense.
Kurtosis = [Σ ni (di – μ)4 / (σ4 N)] / - 3 (σ = std. dev., μ = mean)

This information has been sourced, reviewed and adapted from materials provided by Vision Analytical Inc.
For more information on this source, please visit Vision Analytical Inc.