It has been demonstrated that particles reach a dynamic equilibrium level in normal operating machines. The theory is based on the fact that if particles are generated at a constant rate and are then removed in the system by certain mechanisms such as filters or settling, an equilibrium level is reached when the removal rate equals the production rate. This ceiling value state is not intuitively obvious when setting limits for wear particle analysis by Ferrography and/or Lasernet Fines.
Machine Condition Monitoring by Wear Particle Analysis
The fundamental premise of machine condition monitoring by wear particle analysis is that an abnormal wear mode causes an increase in the size and concentration of wear particles above a previously defined baseline. LaserNet Fines is the ideal tool to establish dynamic equilibrium concentration and hence set alarm limits for any type of machine. Such limits can be set for the type of wear and according to particle size ranges.
Determinig the Difference Between Normal and Abnormal Wear
The figure shows the fundamental difference between spectrometric data and LaserNet Fines data acquired from the same machine as the wear proceeds from Break-In to Normal Wear and finally to Abnormal Wear. The key difference is during the normal wear period. Spectrometric data continues to increase steadily because the particles detected by spectrometers are very small, from particles only a few micrometers in size down to molecular size. These very small particles are not captured by filters or settling. Instead they remain in the oil and accumulate over time. Larger particles, those detected by ferrography and LaserNet Fines, are constantly removed as they are generated. Thus, a dynamic equilibrium exists, unless the wear rate increases or something else happens such as a filter failure.
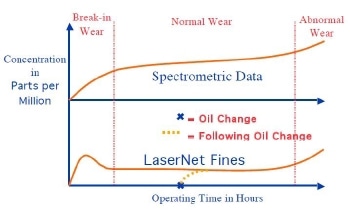
Dynamic Equilibrium for the LaserNet Fines
The practical consequence of dynamic equilibrium is that if samples are taken periodically from a normally running machine, the concentration and size distribution of the wear particles should be more-or-less the same.
In order to determine alarm limits for the LaserNet Fines, a dynamic equilibrium state needs to be established based on a minimum of five samples. The effect of an oil change must be considered because of the time it takes to regain the equilibrium particle concentration as shown in the figure. The characteristic operating time it takes to return to dynamic equilibrium varies with the machine from which samples are taken. Factors which influence operating time to reach equilibrium are:
- Filtration - The better the filter the shorter the time to equilibrium.
- Oil Cycle Rate - The faster the oil cycle rate the quicker the time to equilibrium, some lubricant systems circulate as much as 5 times per minute, while others may only circulate once per hour.
Note: systems like gearboxes that do not circulate the lubricant reach an equilibrium state principally due to settling and comminution (grinding up of particles). The time to achieve equilibrium in gear systems is long compared to circulating systems.
- Particle Size Being Tracked - The larger the particle size range being trended the quicker it will take to reach equilibrium. Large particles are more easily captured by filters than small particles.
Note: Since large particles are so important to incipient failure detection by LaserNet Fines, every effort should be made to take samples before an in-line filter.
Case Study - Determining Dynamic Limit with LaserNet Fines Software
The following example shows how LaserNet Fines software was used to establish a dynamic limit from an equilibrium concentration and to signal an abnormal wear mode to the operator. This is a two step process, first a dynamic equilibrium based on five or more samples is required and second, the limit is calculated and established by the LaserNet Fines software.
Tracking the Dynamic Equilibrium of Sliding Wear Particles
In this example we are tracking dynamic equilibrium of sliding wear particles in the 20-25 µm size range. The first sample is high indicating larger numbers of particles due to break-in wear. After the second sample, the machine appears to have reached a constant state of normal benign wear so a limit will be set based on the equilibrium level as shown in the figure.
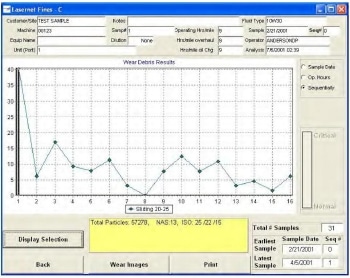
Establishing the Limit for the Sample Trend
The statistical limit is established by the LaserNet software by calculating the standard deviation (sigma [ó]) of the sample range in the selected trend, and recorded as a limit above the mean. The production of wear particles as measured by the LaserNet Fines is a normal distribution, i.e., the concentration is directly proportional to wear rate. Multiples of sigma can thus be used to establish the limit based upon how loose or tight we wish to have the alarm set. The multiple of sigma determines the confidence factor on the number of particles that fall within the mean and the upper alarm limit. A one sigma value provides a 68.7% confidence factor that all the particles above this limit are due to a imminent problem and not due to normal wear. A two sigma value provides a 95.4% confidence factor and a three sigma value a 99.7% confidence factor. The standard deviation multiple used depends on the machine being monitored and the desired confidence factor.
Determining the Limits for Sliding Wear Particles
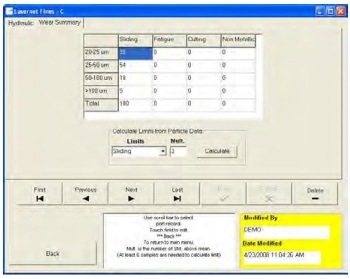
In this case study, a value of 3 sigma was used to calculate the limits for sliding wear particles in four size ranges. The three sigma value gives us 99.7% confidence that any particle concentration recorded above this limit sets of an alarm and any particles that are counted below this limit during sampling are treated as normal wear. The type of wear is selectable from a pull down menu and the size ranges are the normal ones included in LaserNet Fines reports.
The limit for the 20 - 25 µm range of sliding wear particles calculated by the software in this example was 38 particles. The limit is depicted on a trend plot as shown in the left figure and the sample status bar is green indicating the sample is normal. An increase in sliding wear particles exceeded the alarm limit as shown on the following figure.
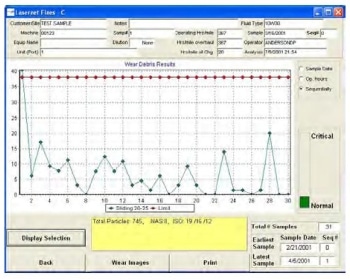
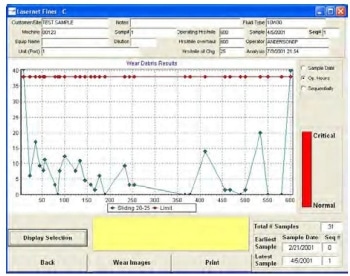
The software warns the user that a critical level of wear has been reached as indicated by the red bar so that corrective action can be taken. Once the problem has been corrected the limit level can be reset and machine monitoring can continue.
Setting the Alarm Limits for the LaserNet Fines Software
Alarm limits can be calculated for all particles above a specified size limit, such as all particles > 4 µm, > 5 µm, > 6 µm, or all counts greater than whatever size that may be desired. Alarm limits can also be calculated for individual particle types such as sliding, fatigue, cutting or nonmetallic.
Summary
LaserNet Fines has been proven to be an excellent tool to establish dynamic equilibrium and to compute statistical limits for various oil applications. The instrument has the unique ability to also image and count particles in heavily sooted diesel engines where this trending technique has been found to be particularly useful.

This information has been sourced, reviewed and adapted from materials provided by AMETEK Spectro Scientific.
For more information on this source, please visit AMETEK Spectro Scientific.