Dynamic equilibrium condition (DEC) is described as a steady-state condition at which the normal wear rate in a machine causes no net gain or loss of particles. The concept of DEC of particles is useful in establishing wear particle limits for all kinds of machinery.
Since OEMs have not set any pre-defined limits, it is often a challenge for the oil analyst or the equipment owner to set condemnation levels for machines producing benign wear particles in large quantities as a result of their normal operation.
End users can set alarm limits for assets with distinctive operating profiles through the knowledge and utilization of dynamic equilibrium models. This article discusses the application of two well-established mathematical models describing this condition to real-world examples that demonstrate the time to equilibrium is not naturally evident. Knowing the level of occurrence of dynamic equilibrium is crucial to understand a normal or an abnormal wear rate for any specific machine.
Anderson-Driver Model for Particle Equilibrium
Anderson and Driver Model shows the achievement of an equilibrium concentration by particles through the summation of a geometric series on the basis of particle production and decay for a specific size and constant wear rate.
When oil is passed through a system as shown in Figure 1, it is assumed that different mechanisms are involved in particle removal, such as filtration, settling, impaction and adhesion, comminution (grinding up of articles), dissolution (oxidation or other chemical attack), and magnetic separation.
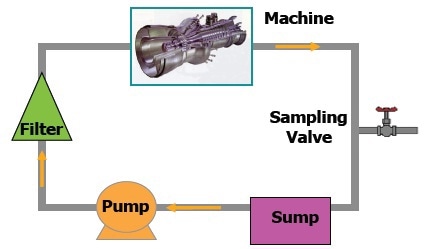
Figure 1. Simplified Oil Path
The model demonstrates the way of summing the geometric series on the basis of the net particle concentration in each cycle to derive a simple formula for the calculation of the time to establish equilibrium under different conditions, as shown in equation 1.
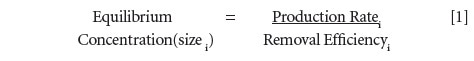
This methodology is utilized to envisage the number of occurrences of oil cycles before attaining an equilibrium level for a given particle size range. This information facilitates the equipment maintainer to determine the correct time to start taking representative samples after an engine overhaul or oil change.
In equation 2, the Anderson-Driver Model determines the number of cycles (R) required to achieve an equilibrium concentration for a specific particle size (ai) and particle loss coefficient (β).
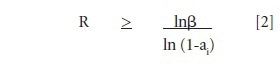
The number of cycles needed to attain 99% of the equilibrium concentrations for values of ai is shown in Table 1.
Table 1. The number of cycles required to reach 99% of equilibrium concentration for given loss coefficients ai
| Number of Cycles |
ai (particle loss coefficient for a given particle size i) |
| 0.8 |
0.1 |
0.05 |
0.01 |
0.001 |
| œ |
1.25 |
10.0 |
20 |
100 |
1000 |
| 3 |
1.24 |
|
|
|
|
| 44 |
|
9.903 |
|
|
|
| 90 |
|
|
19.802 |
|
|
| 459 |
|
|
|
99.007 |
|
| 4603 |
|
|
|
|
990 |
Kjer Model for Particle Equilibrium
Kjer Model shows the variation of the wear particle concentration with respect to time under various conditions and simplified assumptions. The rate of increase in concentration of large particles is given as:
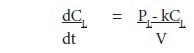
Where:
CL = Concentration of large particles
PL = Production rate of large particles
K = Removal Rate Constant
V = Oil Volume
t = time
Integrating from t=0 and CL = 0, provides large particle concentration as a function of time as follows:
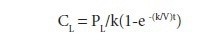
Using the Models to Determine Limits
Taking a diesel engine as an example, these two dynamic equilibrium models can be examined. Both models can be utilized to calculate the predicted time taken by an engine to attain a dynamic equilibrium level for a specific particle size. For both models, particle concentration is exponentially related to time for a specific particle size result.
A typical 40 micron in line engine oil filter commonly used in diesel engines for highway applications is taken for this example. A multi-layer pleated filter will exhibit 90% filter efficiency or better at 40 microns. However, the assumed capture efficiency is 1% for particles in the 4 to 10 micron range. The lube oil pump delivers oil through the filter at a flow rate of 7.5 liters/min. Based on these values, the two models are used to derive time to equilibrium relationships for different engine oil volume capacities as shown in Table 2 and Figure 2.
Table 2. Time to equilibrium for different oil volumes assuming a 1% capture efficiency and 7.5 liter / min filter flow rate.
| |
1% Capture Efficiency (4-10 mm particles) |
Time to Ec |
uilibrium |
| Anderson Driver |
Kjer |
| Oil Volume (liters) |
Flow Rate(L/hr) |
# Cyc |
Total vol through the filter |
Time (hrs) |
Time (hrs) 63.2% |
| 40 |
450 |
459 |
18360 |
41 |
9 |
| 20 |
450 |
459 |
9180 |
20 |
4.5 |
| 10 |
450 |
459 |
4590 |
10 |
2 |
| 5 |
450 |
459 |
2295 |
5 |
1 |
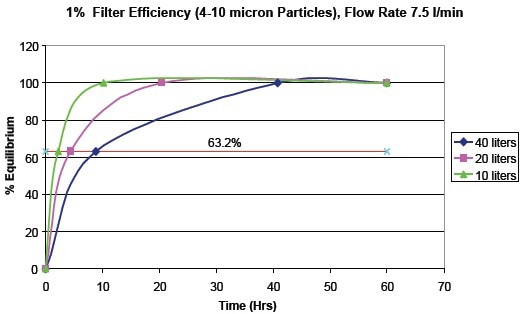
Figure 2. Combined time to equilibrium models for different oil volumes derived from Table 2.
This simple diesel engine example demonstrates the impact of particle size, filtration efficiency, oil flow rate, and oil volume capacity on the time to equilibrium.
Establishing Limits Using DEC
The basic principle of wear particle analysis for machine condition monitoring is that an abnormal wear mode increases the size and concentration of wear particles above an already defined baseline. It is possible to set such limits for the wear type based on particle size ranges. The practical consequence of DEC is that the size distribution and concentration of the wear particles taken periodically from a running machine must be constant.
To set alarm limits for a specific machine, it is necessary to establish a dynamic equilibrium state based on at least five samples. It is also necessary to take into account the effect of an oil change as it takes some time to regain the equilibrium particle concentration. The characteristic operating time taken by it to regain the dynamic equilibrium differs with the machine from which samples are collected.
Conclusion
Although both dynamic equilibrium and particle behavior in a machine are not clearly evident at first, they are essential for the equipment owner to predict the time of occurrence of an abnormal wear mode. They also help the oil analyst to predict when to collect a sample between an engine overhaul or oil change depending on certain operating parameters. It is necessary to closely track large particles as they signal the occurrence of increased wear rate and abnormal wear mode in a machine. The DEC concept is useful in applications such as complex lubrication systems, wind turbine gearboxes, and large diesel engines.

This information has been sourced, reviewed and adapted from materials provided by AMETEK Spectro Scientific.
For more information on this source, please visit AMETEK Spectro Scientific.