Dynamic Light Scattering (DLS), also known as Quasi-Elastic Light Scattering (QELS) or Photon Correlation Spectroscopy (PCS), is a widely applied method to measure the size of particles dispersed in a liquid.

Image Credits: HQuality/shutterstock.com
DLS determines the Brownian motion of the particles suspended in the liquid. Embedded probe particle microrheology methods are based on DLS.
Newtonian System
There is a linear increment in the Mean Square Displacement (MSD) with time for a particle that moves freely because of thermal fluctuations in a Newtonian fluid and the slope of this increment is represented by the diffusion coefficient of the particle as follows:
Where,
⟨Δr2(t)⟩ is the MSD,
d is the dimensionality of the motion (2 for motion in a plane, 3 for motion in space), and
D is the diffusion coefficient of the particle.
In a Newtonian system, the Stokes-Einstein relationship can be used to represent the diffusion coefficient as a function of the viscosity of the fluid medium, the size of the particle, and the temperature as follows:
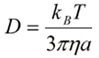 |
(2) |
Where,
α is the diameter of the particle,
η is the viscosity of the fluid medium,
T is the temperature, and kB is the Boltzmann constant. Hence the MSD of the particle can be correlated to the viscosity of the fluid using the Stokes-Einstein equation.
The Generalized Langevin Equation
The complete nature of a viscoelastic (non-Newtonian) complex fluid can be described using Equation (2) because the medium shows both storage of energy (elasticity) and dissipation of energy (viscosity). Particle motion becomes sub-diffusive and the slope of the MSD becomes nonlinear when the suspending medium’s elasticity becomes significant.
The corroboration of a more general method to extend the strategy of correlating MSD for the measurement of the linear viscoelastic moduli of complex fluids utilizing DLS is the cornerstone of modern Microrheology. The thermally-driven motion of a particle dispersed in a complex fluid can be described using the generalized Langevin equation as follows:
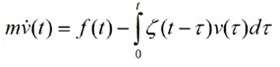 |
(3) |
Where,
m is the mass of the particle,
ν is the particle acceleration,
f is the total force acting on the particle, and Z is a time-dependent memory function accounting for the elasticity in the system.
The Generalized Stokes-Einstein Relation
The Generalized Stokes-Einstein Relation can be derived by solving the equation of motion for the case where the particle motion is thermally driven. This links the tracer’s MSD to the viscoelastic modulus of the complex fluid medium that surrounds the particle as follows:
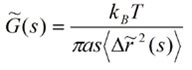 |
(4) |
Where,
the tilde symbol is the Laplace transformation, and s is the Laplace frequency
If G* is the viscoelastic modulus of the system as experienced by the probe particle, then Equation (4) Equation (4) can be recast in Fourier space by utilizing the identity s=iω as follows:
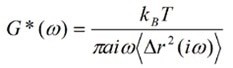 |
(5) |
Where the angular frequency ω is defined as ω=2π/t.
Assuming the complex fluid medium as a continuum around the particle is the basis of the Generalized Stokes-Einstein Relation, i.e., the length scales of the microstructures in the complex fluid are tinier when compared to the particle size.
Rheological Data Extraction from DLS Measurements
A DLS experiment measures the auto-correlation function (ACF) of the light scattered by particles experiencing thermally-driven motion within a material being studied. The ACF, g1(τ), can be defined as a function of the MSD of the scattering particles as follows:
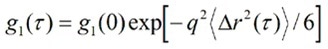 |
(6) |
where g1(0) is the value of ACF at zero time (or intercept), and q is the scattering vector defined as follows:
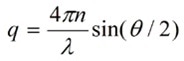 |
(7) |
Where,
n is the refractive index of the medium,
λ is the wavelength of the light and θ is the scattering angle. The correlation time τ is linked to the time t as: τ=2π/t, so that ω=I/τ
Hence, probe (tracer) particles of a known size need to used in a DLS Microrheology experiment to measure the ACF of the light scattered by the probe particles. Then the MSD of the probe particles can be correlated to the ACF of the scattered light using Equation (6) as follows:
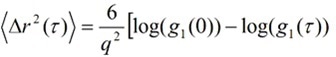 |
(8) |
Where,
g1(0) is the estimated intercept of the value of the auto-correlation function, and q is the scattering vector. Calculating and substituting the Fourier transform of the MSD in Equation (5) yields the viscoelastic modulus. An approach based on a power law expansion of the MSD is used to estimate the complex shear modulus algebraically by expanding ⟨Δr2(t)⟩ locally around t = 1/ω to yield:
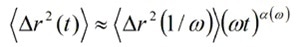 |
(9) |
Where ⟨Δr2(1/ω)⟩ is the magnitude of ⟨Δr2(t)⟩ at t = 1/ω and α(ω) is the power law exponent that describes the logarithmic slope of ⟨Δr2(t)⟩ at t = 1/ω as follows:
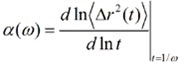 |
(10) |
If the probe particles experience thermally driven motion, then the slope of the logarithmic time derivative of the MSD will be zero in an elastic medium (completed arrested motion), one in a purely viscous medium (diffusive motion), and will lie between these extremes in a complex viscoelastic fluid medium.
The Fourier transform of the power law behavior of the MSD is evaluated by substituting into Equation (5). Expressions for the frequency-dependent viscoelastic moduli - G', elastic (storage) modulus and G'', viscous (loss) modulus can be obtained using Euler’s equation as follows:
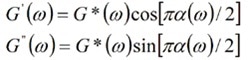 |
(11) |
Where,
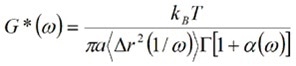 |
(12) |
Here, Γ represents the gamma function due to the Fourier transform of the power law behavior of the MSD. Then complex viscosity, η*, can be defined as:
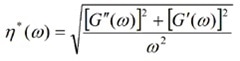 |
(13) |
Applicability of DLS Microrheology
The conditions, where either DLS measurements or the assumptions within the Generalized Stokes-Einstein Relation become unreliable, need to be considered to obtain robust and consistent DLS Microrheology data. Appropriate data quality requirements can be highlighted by means of certain quality criteria that can be applied, for example to ACF. In addition, defined method development procedures need to be used to perform valid DLS Microrheology measurements.
Microrheology techniques are based on the Generalized Stokes-Einstein Relation, which is applicable to a wide range of complex fluid types, thus facilitating the measurement of quantitative rheological data across a wide range of frequencies. Nevertheless, the following are the instances where assumptions within the Generalized Stokes-Einstein Relation can fail, and where Microrheology data and bulk rheological measurements are not in good agreement:
- Influence of probe particle-matrix interactions
- Influence of probe particle size and material heterogeneity
- Materials with evolving or aging microstructure
- Aggregating or gelling systems close to the gel point

This information has been sourced, reviewed and adapted from materials provided by Malvern Panalytical.
For more information on this source, please visit Malvern Panalytical.