Using Practical Pneumatic Isolators without Compromising Small Amplitude Vibration Isolation Performance

Figure 1 displays a cutaway view of TMC’s Gimbal Piston™ isolator, which uses two air chambers instead of one. The chambers are connected by a small orifice. When the piston moves up and down, air is forced to pass through the orifice, generating a damping force on the payload.

The damping is very strong for large displacements of the piston and weak for the smaller ones. This enables fast settling of the payload, without compromising the performance of small amplitude vibration isolation. This type of damping generally produces a Q ≈ 3 for displacements on the order of a few millimeters.

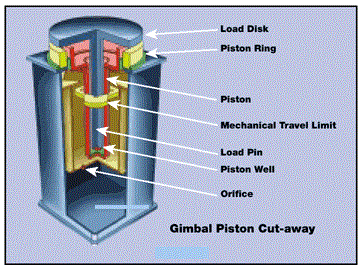
Figure 1.

The damping provided by an orifice is constrained by many factors. TMC’s MaxDamp^® isolators use a different method: multi-axis viscous fluid damping (Patent No. 5,918,862). These isolators extend the damping to near-critical levels for applications that require it.

For instance, semiconductor inspection equipment frequently uses rapid moving stages to transport wafers. MaxDamp^® isolators permit the payload to settle quickly post-a stage motion even when offering significant amounts of vibration isolation.

The isolator uses an extremely low outgassing, synthetic oil with high-viscosity, which is hermetically sealing inside the isolator’s single air chamber. A special geometry ensures that the isolator damps both vertical and horizontal motions (in X and Y directions) with the same efficiency.

The Gimbal Piston™ and MaxDamp^® isolators have a robust and simple pendulum isolator to provide horizontal isolation. Similar to air springs, pendulums also produce an ω₀, which is not payload-dependent, and equal to √g/l, where l is the pendulum length.

In the Gimbal Piston™, the pendulum is actually the piston. The payload is supported by a load disk, which transfers its burden to the bottom of the piston well via the load pin. The load pin is in contact with the bottom of the piston well through a pivoting thrust bearing.

When the payload moves sideways, the piston well pivots like a gimbal in the plane of the diaphragm. Hence, a pendulum is formed, whose length is equal to the vertical distance from the roll in the diaphragm to the bottom of the load pin.

TMC’s Compact Sub-Hertz Pendulum (CSP^®) System (Patent No. 5,779,010) uses a different type of pendulum concept to extend horizontal resonant frequencies down to as low as 0.3 Hz. In this isolator, a geometrical lever effect is used to “fold” a 0.3 Hz pendulum into a package which is less than 16 in. (400 mm) high.

An equivalent simple pendulum needs to be 110 in. (almost 3 m) tall. For more information, readers can visit TMC’s Pneumatic Vibration Isolators for OEM Applications page.

In most isolators, horizontal damping comes from horizontal-to-tilt coupling. As a payload moves sideways, it exercises the isolators in the vertical direction (through tilt), providing damping. Some systems such as TMC’s MaxDamp^® isolators, damp horizontal motions with fluidic damping.

At small amplitudes, small amounts of friction in the rolling diaphragm and the low resistance to flow due to the damping orifice impact the isolator’s performance. This is the reason that it is important to use smaller excitation levels when measuring their transmissibility.

Number and Placement of Isolators

Three or more isolators are required to support a payload, the common number being four. Since a system can have only three valves (see section Leveling Valves), two legs in a 4-post system need to be connected as a master/slave combination.

Although a master/slave combination forms an effective support point, the resulting damping effect is much different from that if a single (larger) isolator was used. TMC’s recommendations include using a minimum of four isolators (except for “round” payloads like NMR spectrometers). Placing these isolators under a payload has a significant effect on the systems’ performance.

For small rigid payloads, such as the granite structures in semiconductor manufacturing equipment, it is advisable that the isolators are placed proximal to the corners of the payload. This greatly enhances the tilt stability of the system, reduces the payload motions caused by onboard disturbances, and improves the leveling and settling times for the system.

Leveling time is defined as the time for the valving system to bring the payload to the correct height and tilt. Settling time is known as the time for a payload to come to rest after an impulse disturbance.

In the case of extended surfaces, including large optical tables, the isolators need to be placed under the surface’s nodal lines to minimize the effect of forces conveyed to the table by the isolators. For both types of payloads, it is better to position the payload’s center-of-mass in the same plane as the isolator’s effective support points. This enhances the system’s stability (see section Gravitational Instability) and delinks the payload’s horizontal and tilt motions.

Several techniques exist to accommodate uneven floors. Most TMC isolators have a ±0.5 in. travel range, providing sufficient flexibility for nearly all applications. Some systems provide leveling feet. If a floor is very uneven, piers for the isolators may be needed.

Some of the free-standing isolators or supports like rigid tripods need to be grouted to the floor if the floor has a poor surface quality. Quick-setting “ready-mix” concretes or epoxies are suitable for such situations.

Safety Features

Pneumatic isolators can easily lift payloads weighing several thousand pounds. Isolators can be tied together with “tiebars,” so that the risk of toppling such heavy loads by accident or by events such as earthquakes is greatly reduced. TMC’s tiebars are heavy-gauge, formed channels, which use constrained-layer damping to prevent them from resonating.

Such damping may not be needed, due to the high isolation efficiency of the isolators at those frequencies. Additionally, systems can be provided with earthquake-restraint brackets for preventing the payload from shaking off the isolators in extreme events.

The travel limits built into all TMC’s isolators are important safety features. In Figure 1, an internal “key” (yellow) prevents the system from overextending even when pressurized to 120 psi (830 kPa) under “no load” conditions.

As there can be several thousand pounds of force acting on the isolator’s piston, an isolator devoid of a travel limit can turn into a cannon when suddenly unloaded. Protection including chain-linked pressure reliefs, does not offer the intrinsically high safety level that a mechanical travel limit does.

Leveling Valves

Only three height control valves are used for all rigid payloads, even those with ten isolators. As three points define a plane, using more valves would mechanically over-constrain the system and lead to poor position stability (like a four-legged restaurant table) and non-stop air consumption. Appropriate placement and plumbing of the three valves is critical to optimize the system’s performance.

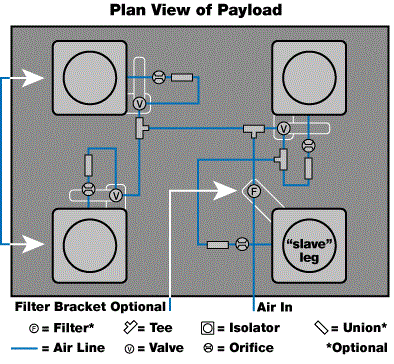
Figure 2a.

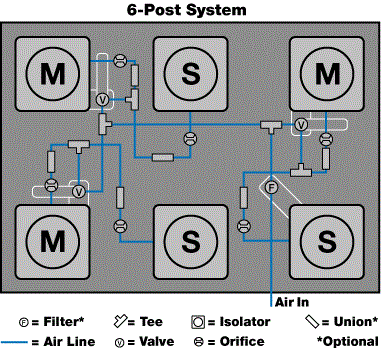
Figure 2b.

Figures 2a and 2b display the common plumbing for a 4-post and 6-post system. A system consists of three valves, a pressure regulator/filter (optional), some quick-connect tees, and an orifice “pigtail” on each isolator, which is a short section of tubing with an orifice inserted inside.

A red ring is marked on the section, which has a union on one end to connect to the air lines of the height control valves. The orifices restrict the “gain” of the servo (mechanical valving system) to prevent oscillation. Some of the high center-of-gravity systems may need smaller orifices to prevent instabilities. TMC uses fixed orifices instead of adjustable needle valves due to their ease of use and long-term stability.

For a system with four or more isolators, two or more of the isolators need to be tied together. Generally, the valve is mounted close to an isolator (for convenience) and that isolator is known as “master.” The remote isolators (S) that use the master valve are called “slaves.”

The selection of legs as “master” and “slave” influences the system’s stability (see section Gravitational Instability) and impacts a system’s dynamic behavior. Dynamic performance is very important in semiconductor inspection machines which have fast moving stages.

There are many “rules of thumb” that can be applied to make the right choice, although they can conflict with one another on a few systems. Some experimentation may be needed to determine the optimal choice.

These rules, in approximate order of importance, are:

1. The effective support point for a master and its slaves lies at their geometric centers. For a master with a single slave, the geometric center is midway between the mounts. There are always only three “effective” support points for any system, and connecting the points forms a “load triangle.” The system will be more stable if the payload’s center-of-mass (COM) is close to the center of the triangle. For instance, on a 4-post system, the master/slave combination needs to support the lighter end of the payload.
2. A corollary to rule #1 is that the system needs to be plumbed so that the pressure difference between all isolators is minimized.
3. A system’s gravitational tilt stability is proportional to the square of the distance between the isolators. So, for better stability, the master/slave combinations need to be on the long side of a payload.
4. The tilt axis with the highest stiffness, stability, and damping is parallel to the line between the master and slave legs (in a 4-post system). For moving stage applications, the main stage motion needs to be perpendicular to the line between the master and slave leg.
5. A cross-axis tilt can be caused by a moving stage because the valve for the master/slave legs is not co-located with the effective support point. Accordingly, in many systems, the valve needs to be moved from the master leg to the effective support point.
6. The three points of contact of the valves with the payload form a control triangle. Similar to the load triangle, the system has the greatest stability and best positioning accuracy if the COM is inside the control triangle. The valves must be mounted and their “arms” rotated so that the triangle has the largest possible area.
7. Following the above rules can sometimes result in a system having poor height and tilt positioning accuracy. In such a case, an alternative choice for the master/slave combination(s) may be required.

In addition to valve location, there are several different types of valves available. TMC provides standard mechanical valves and precision mechanical valves. The standard valve is cheaper and has a positioning accuracy (dead band) of about 0.1 in. (2.5 mm).

It has the property that the valve is tightly sealed for motions smaller than this. This makes it suitable for systems that need to use pressurized gas bottles for an air supply. Precision valves provide a 0.01 in. (0.3 mm) or better positioning accuracy, but leak a small quantity of air (all-metal valve seats are used internally).

This limits their use for gas bottle operation. Finally, TMC provides electronic valving systems such as the Precision Electronic Positioning System (PEPS^®), U.S. Patent No. 5,832,806), which has about 0.0001 in. (approximately 2 µm) position stability. For more information, readers can visit TMC’s PEPS and PEPS-VX pages.

For cleanroom applications, TMC provides stainless steel mechanical valves and/or supplied with a vented exhaust line.

Gravitational Instability

Similar to a pen balanced on its tip, payloads supported below their COM are inherently unstable. As the payload tilts, its COM shifts horizontally in a way that further increases the tilt. Counteracting this is the stiffness of the pneumatic isolators, which try to restore the payload to a level position.

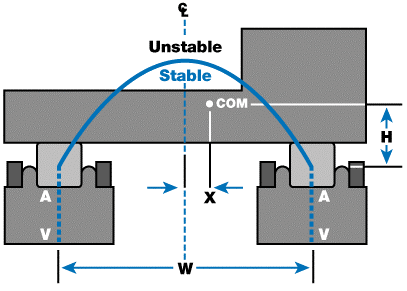
Figure 3.

The balance of the two forces determines the system’s gravitational stability. Figure 3 illustrates a payload that is supported by two idealized pneumatic isolators. W is the width between the centers of isolators, H is the height of the payload’s COM above the effective support point for the isolators, and X is the horizontal position of the COM from the centerline between the isolators. The region of stability is expressed as:

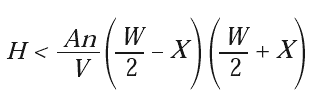[1]

or, for X = 0,

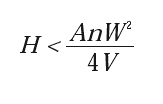[2]

where n is the gas constant equal to 1.4.

This relationship is illustrated in Figure 3 as an inverted parabola defining the stable and unstable regions for the COM location. The second equation shows that the stability is enhanced with the square of the isolator separation.

This is critical as it shows that the aspect ratio H/W does not determine the stability of a system (as claimed by some references) and that the stable region is not a “pyramid” or “triangle.” However, real systems are not as simple as the one shown in Figure 3.

The ratio A/V in Equations 1 and 2 represents the stiffness of the isolators . However in a two-chamber isolator, what is the proper V? Unlike the isolators shown in Figure 3 that have a fixed spring constant, real isolators possess a frequency-dependent spring constant.

At high frequencies, the orifice between the two chambers successfully blocks air flow, and V can be taken as the top air volume alone. At the system’s resonance, the “effective” air volume exists between the top and total (top plus bottom) volumes. At low frequencies, the height control valves provide a very high stiffness (corresponding to a very small V) to the isolators.

Additionally, the height control valves also try to force the payload back towards level. These are some of the reasons why Equation 1 cannot be applied to the two-chamber isolators.

Instead, three regions, stable, unstable, and borderline, can be assigned; the first two being based on the “total” and “top-only” air volumes, respectively. Also, the stability region differs for the axes parallel and perpendicular to the master/slave isolator axis.

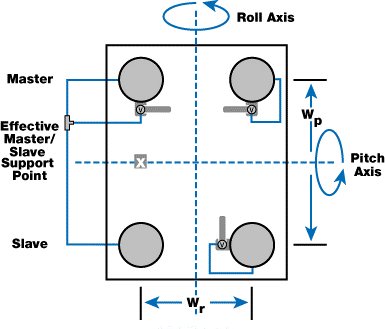
Figure 4.

Figure 4 defines the two different axes for a four-leg system. The pitch axis is less stable because the master/slave legs on the left offer no resistance to pitch at low frequencies (although they do resist pitch at frequencies above approximately 1 Hz).

To compensate for this, the master/slave combination is selected in such a manner that W_p is greater than W_r (rule 3 from section Leveling Valves). The region of stability is the volume covered by the inverted parabolas along the two axes.

The formula for absolute stability is:

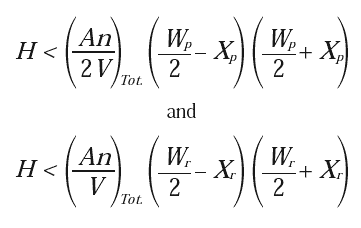[3]

and the formula for absolute instability is:

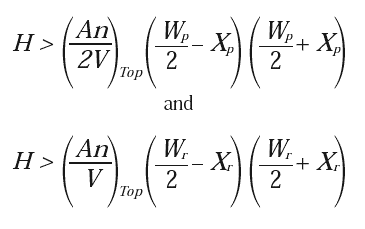[4]

with the volume between being “marginally” or “possibly” stable.

The ratios A/V are not universal and need to be confirmed for various models and capacities of isolators but are approximately 0.1 in^–1 for (A/V)_Top and 0.05 in^–1 for (A/V)_Tot. Figure 5 shows what the marginally stable region looks like for two-chamber isolators.

Unfortunately, the COM of many systems ends up in this indeterminate region. These rules do not account for the actions of the height control valves, which will always improve the stability of a system. These rules can change if the payload has a mass that can shift (a pendulum or a liquid bath).

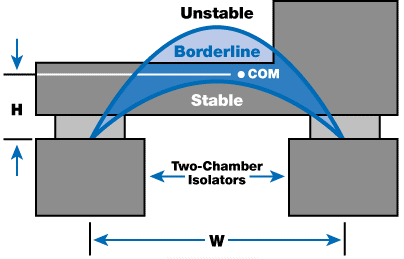
Figure 5.

Equations 5 and 6 give “rules of thumb” to calculate a system’s stability. As with all such rules, the system’s stability is only an approximation based on an “average” isolation system. It is always better to use a low COM.

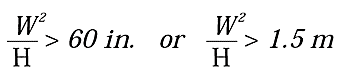[5]

MaxDamp^® isolators are more stable as they use a single air chamber, and accordingly, the rule is:

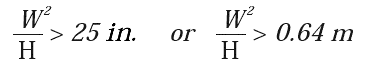[6]

The effective support point for TMC’s Gimbal Piston™ isolators is about 7 in. below the top of the isolator. For lightly loaded isolators, these conditions underestimate the stability of a system. If a system violates these equations, or is a borderline case, the stability can be enhanced by using special volume isolators, counterweights, different isolator valving, etc.

This information has been sourced, reviewed and adapted from materials provided by TMC.

For more information on this source, please visit TMC.