Analysis of Polymers by Oscillatory Indentation

A common technique used to characterize the mechanical properties of bulk polymer specimens is known as DMA or Dynamic Mechanical Analysis. It is a technique in which oscillatory stress is placed on the sample regarding tension, compression or torsion and the resulting strain is measured. The outcome is the storage modulus, E’, which denotes the polymer's ability to store energy elastically and the loss modulus, E’’, which denotes the polymer's ability to dissipate energy. Combined E’ and E’’ are the complex modulus of the material.

Phasor analysis of DMA mechanics shows that the storage and loss modulus is concisely related via the loss factor, which is the tangent of the phase angle, δ, by which the strain lags the stress, i.e.,

In practice E’, E’’ and tan δ are measured as a function of frequency and temperature in DMA. If two parameters are known the third can be identified.

Suppose a sample volume is too small for a DMA test, analogous measurements can be made using an oscillatory indentation test. An indenter is pressed into the sample and an oscillating force is imposed. The resulting displacement oscillation is measured and interpreted in the light of established contact models, and equivalent measurements of E’ and E’’ can be obtained.

Oscillatory indentation may work better than DMA testing even if the volume of the sample is larger. The moving mass of an indenter is much smaller than the moving mass of a traditional DMA instrument, which means that the indenter can be made to oscillate at much higher frequencies. Thus, an oscillatory indentation can be used to characterize a larger frequency range than DMA. Also the temperature of that volume can be changed faster, and with less heat, relative to DMA if the volume is smaller. Lastly, the preparation of sample for indentation testing is easier in oscillatory indentation than in DMA.

Theory

The behind oscillatory indentation is based on both elastic contact models and constitutive forms used to comprehend the mechanical behavior of polymers in DMA testing. The general relation between force, displacement, and elastic modulus for an axisymmetric indenter in contact with a flat surface was first derived by Ian Sneddon. Further on Oliver, Pharr, and Brotzen showed that a derivative form of Sneddon’s relation is actually independent of the geometry of the indenter. The derivative is commonly used to interpret instrumented data. It is represented by

(2)

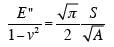Here E’ is the storage modulus of the material, ν is the Poisson’s ratio, S is the elastic stiffness of the contact and A is the contact area. If the material being tested has a substantially elastic response, the storage modulus is identical to the better known Young’s modulus, E. An analogous relationship between the loss modulus, E”, and contact damping, D_s ω was invoked by Loubet, Lucas, and Oliver.

(3)

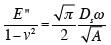For oscillatory indentation, the loss factor is particularly advantageous, because the contact area is eliminated as an unknown.

Thus, the task of measuring the complex modulus of a polymer by oscillatory indentation is that of measuring the contact stiffness, S, and contact damping, D_s ω

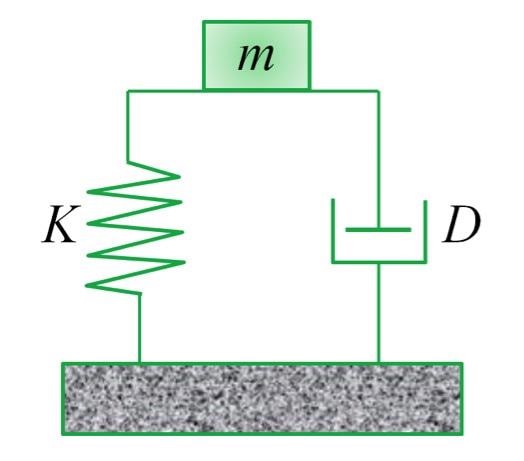
Figure 1. Simple harmonic oscillator used to model the indentation system alone or in contact with a sample.

The iNano indentation system manufactured by Nanomechanics, Inc. has been designed to act like a simple-harmonic oscillator so that by oscillating the system with a force amplitude, F₀, and angular frequency, ω, and measuring the resulting displacement amplitude, z₀, and phase shift, φ, we may know the values of all the components of the model: K, D, and m. It is seen as

(5) (6)

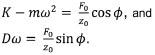If the indenter is not in contact with any material, then K, D, and m are the stiffness, damping, and mass of the indentation system alone, or K_i, D_i, and m_i. These values are determined in a factory calibration by oscillating the indenter when it is free-hanging. If the indenter is touching a test material the parameters K, D, and m comprehend the combined effect of both the indentation system and the contact making it necessary to compensate the fundamental values of F₀, z₀, and φ. In an experiment we obtain the contact stiffness for use in Eq. 2 as the combined stiffness less the instrument stiffness,

(7)

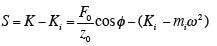and we obtain the contact damping for use in Eq. 3 as the combined damping less the instrument damping, or

(8)

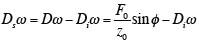Flat-ended cylindrical tips have an advantage when testing polymers as they promote deformation that is consistent with the assumption of linear viscoelasticity, and the contact area is known and independent of penetration depth. A punch diameter’s selection is based on considerations of microstructure, desired spatial resolution, material properties, and the sensitivity and capacity of the testing instrument. The punch face should be large enough to cover relevant features that determine mechanical behavior, but the punch must not be so large that the instrument cannot provide enough force to bring the punch face into full contact with the test material and then oscillate.

Experimental Method

Plasticized polyvinyl chloride (HP-PVC) which is sold commercially as a mat to dampen noise and vibration were tested. It was a small square of approximately 15 cm on a side and 6 mm thickness. A small section was potted in epoxy and metallographically polished. The iNano indentation system was used to measure the complex modulus as a function of frequency. The system produced by Nanomechanics, Inc. was fitted with a 60o frustum having a face diameter of 52.5 μm. Testing was at room temperature using “Dynamic Flat Punch Complex Modulus” method.

Figure 2. Simple harmonic oscillator used to model the indentation system alone or in contact with a sample.

Steps followed automatically at each test site included:

1. Bringing indenter face in full contact with the surface

2. Measurement of amplitude of the force oscillation (F₀) which would cause a displacement oscillation (z₀) of about 50 nm at 100 Hz was fixed. Once determined, _F0 was fixed for the remainder of the test

3. The system sequentially imposed the prescribed frequencies, ω, and measured the resulting displacement oscillation, z₀, and phase shift, φ, at each frequency.

4. Calculations were made for contact stiffness and damping for each frequency, as well as the storage modulus, loss modulus, and loss factor.

The experiment saw the process above being repeated 15 times over different test sites on the surface of the sample.

Results and Discussion

The results from oscillatory indentation were compared to those obtained by tests on another sample of the same material using DMA. The measurements were repeated with very little standard deviation. Given the profound differences in equipment and sample geometry, the agreement between oscillatory indentation and DMA is outstanding.

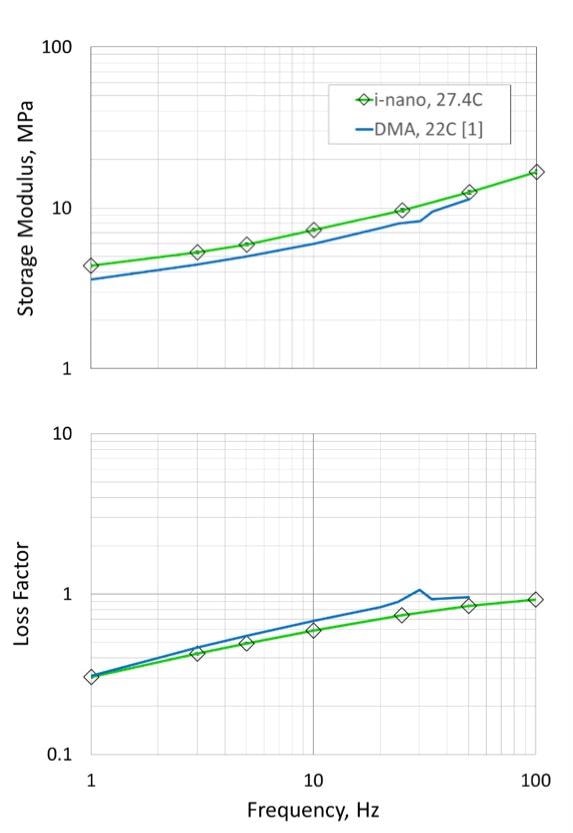
Figure 3. Storage modulus (top) and loss factor (bottom) of highly plasticized polyvinyl chloride as measured by oscillatory indentation (green trace) and dynamic mechanical analysis (blue trace).

The properties for the HP-PVC are a strong function of frequency. As expected, the loss factor (tan δ) for this material is particularly high. At higher frequencies, the loss factor approaches unity, which means that the material damps out as much energy as it stores and returns elastically.

In the HP-PVC, the loss factor increases sharply with frequency over the testing domain. This implies that the material is approaching (in frequency space) a phase transition. Peaks in the loss factor (tan δ) as a function of frequency or temperature imply phase transitions in the material, such as the glass transition.

Conclusion

A number of variables affect the mechanical properties. Oscillatory indentation allows testing of small volumes of material in a very relevant manner with minimal sample preparation effort. The iNano indentation system produced by Nanomechanics, Inc. can measure complex modulus as a function of frequency. The results are comparable to those achieved by the DMA over the same domain.

References

1. Herbert, E.G., Oliver, W.C., and Pharr, G.M., ‘‘Nanoindentation and the Dynamic Characterization of Viscoelastic Solids,’’ Journal of Physics D: Applied Physics 41:1–9 (2008).
2. Sneddon, I.N., ‘‘The Relation Between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile,’’ International Journal of Engineering Science 3:47–56 (1965).
3. Pharr, G.M., Oliver, W.C., and Brotzen, F.R., “On the Generality of the Relationship Among Contact Stiffness, Contact Area, and Elastic Modulus During Indentation, Journal of Materials Research 7(3):613–617 (1992).
4. Loubet, J.-L., Lucas, B.N., and Oliver, W.C., ‘‘Some Measurements of Viscoelastic Properties with the Help of Nanoindentation,’’ NIST Special Publication 896 31(1995).

This information has been sourced, reviewed and adapted from materials provided by Nanomechanics, Inc.

For more information on this source, please visit Nanomechanics, Inc.