What is DLS and how is it used to determine particle size?
To begin, a laser is cast upon the sample cell. The sample scatters a fraction of that light into an optical fiber, which then goes into an avalanche photodiode. This diode tracks the scattered light intensity as a function of time. This is then fed into a correlator board, which creates the correlation function.
What exactly is creating these fluctuations in light intensity? To understand this, we have to think about what exactly is happening inside the sample solution. Let's imagine that at time zero we have two particles positioned such that the light waves from each particle are being scattered is in sync, meaning the photodiode receives constructive interference and therefore a larger voltage signal. However, let's now imagine a little time later where these two particles have diffused a bit apart. Now the scattered waves are out of sync with each other. Therefore, the diode receives a lower voltage because there's destructive interference occurring. The main takeaway is that fluctuations in light intensity over time are due to Brownian motion of these particles.
The rate of fluctuations in light intensity differ depending on particle size. Small particles diffuse very quickly, and as a result we see fast fluctuations in the light intensity. This causes the correlation function to decay over a short time scale. In contrast, large particles diffuse more slowly. As a result, the fluctuation in light intensities happens at a slower rate and the correlation function decays over a longer time scale.
What if a solution contains multiple particles of different sizes?
Real samples often have aggregates, and they might also have multiple populations of particles in solution. So a common question that arises is, which model do I use to determine my particle size? Let us begin first with a simple example; one in which all the particles sizes are the same. To describe the solution, we would say that it's monomodal and monodisperse. Its correlation function would have a single exponential decay and the model that we would use to describe it is called the method of cumulants; the cumulants model uses only a single exponential decay.
Now let's move to a sample that's a little bit more complex: a solution that forms dimers and oligomers in addition to monomers. In this example, we would still describe it as monomodal, but we would also now say that it's polydisperse because there's a little bit of variability in diameter. In this example, it is still appropriate to use the cumulants model but we would use the polydispersity index to interpret the deviation from a pure, monodisperse sample.
Next, let's consider an example where we have two different populations that are very different in size, but each population of samples would be considered monodisperse. In this case, we would call it multimodal. As there are two different populations, what happens with the correlation function is that we see two decay times, one for the smaller species and a second for the larger species. In this case, it is not appropriate to use the cumulant model. Instead, we need the regularization model because the regularization model fits an arbitrary number of populations with different mean sizes.
Finally, let's consider an even more complex solution where we have two different distinct species and those two species have polydispersity within them. In this case, the solution would be described as multimodal and polydisperse and we would also be using the regularization model. The polydispersity index is calculated for each population.
What technology is available from Wyatt that can determine particle size?
Wyatt Technology has three different detectors that can measure particle size. One is the DynaPro Plate Reader, which measures size and molar mass in a microwell-plate format. The DynaPro NanoStar measures size and molar mass in a quartz cuvette or a plastic disposable cuvette. Finally, the Mobius measures particle size and zeta potential in either a quartz cuvette or a PEEK flow cell.
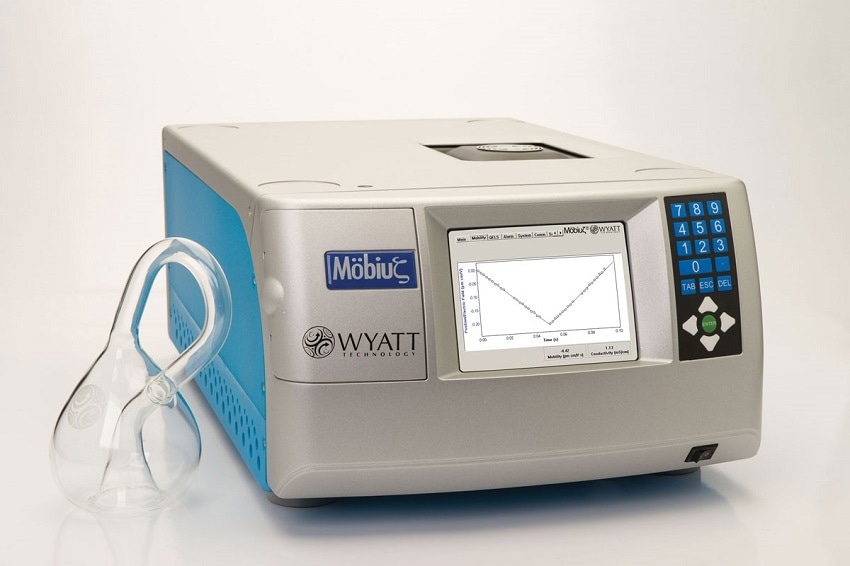
How does the Mobius calculate particle size and zeta potential?
The Mobius measures PALS to calculate the mobility of particles. The unit uses a high-power, 50-milliwatt, 532 nanometer laser to illuminate the sample cell. For PALS analysis, the scattered light is collected by 31 independent diodes. In the sample cell, we have the two platinum electrodes and let's just assume that the left platinum electrode is polarized negatively. Let's also assume that the particles in solution have a net positive charge. In this case, the particles will move in the leftward direction. As a consequence of this movement, the wavelength of light received by the right half of the diodes will be redshifted. However, the wavelength received by the left half of the detectors would be slightly blue-shifted. This shift is proportional to the net surface charge and the total charge of the particle. However, this shift is very difficult to detect. It's very small.
The method that is used to detect this small change is called interferometry. In this case, we take a fraction of the original laser light and recombine it with the scattered light; this creates a beat pattern, detected over time by the photodiodes. The frequency of this beat pattern is then used to calculate the mobility; however, mobility alone isn't sufficient to calculate the zeta potential. An accurate calculation of zeta potential requires knowledge of not only the mobility but also the particle size. For that reason, there is a built-in DLS detector in the Mobius unit. This allows us to measure mobility and particle size in the same scattering volume at the same time, so there is no need to switch any cell or re-measure the sample.
The accurate measurement of zeta potential requires simultaneous DLS and PALS measurements in the same sample cell.

How are PALS data typically presented?
PALS data are displayed in a V-graph. The y axis denotes electrophoresis per unit electrical field (you could think about this as the distance moved per electrical field applied) and the x axis represents time. The slope of the plotted points is actually the measure of electrophoretic mobility. If we were to increase the surface charge of our particles, the slope of the line and also the mobility would increase.
Another useful aspect of V-graphs is that its direction tells us about the net surface charge. If the V-graph points in a downwards direction we know that the net surface charge is negative. However, if this V-graph points in the upwards direction, we would know that our net surface charge is positive.
What conditions can make measuring the zeta potential more difficult?
A sample property that can cause complications to the measurement of zeta potential is conductive buffer. Even 10 millimolar of NaCl can cause complications. One complication is the formation of bubbles by electrolysis. This would basically impact the field being applied, and therefore lead to an incorrect mobility value.
A second complication due to high salt is dielectrical shielding by the ions themselves. The effect of this is that the particles of interest will feel the field less, and therefore move less, leading to an underestimation of the mobility.
Another thing that salt ions can do is change the model that should be used to calculate zeta potential. For example, the Hückel model should be used when you have samples of small particles in a low-salt solution. However, the Smoluchowski model should be used when you have large particles in a high-salt solution. The error in the zeta potential could be as high as 50% if you were to select the wrong model.
How does Wyatt’s technology overcome these difficulties?
In regards to solutions, bubbles can be overcome by using the Atlas accessory which can pressurize the flow cell to 500 psi, driving the bubbles back into solution.
In regards to the challenge of dielectrical shielding, what can be done is to switch to a higher field frequency. So instead of using 10 hertz, we typically use 20 hertz for highly conductive samples.
In real samples, particle size and solution salinity are somewhere between the Hückel and Smoluchowski models. For this reason, the Mobius software has a third model called the Henry model. In this model, we are able to plug in the ionic strength of our buffer. The software will then calculate the exact function that should be used to calculate the zeta potential. If you do not know the ionic strength, there is also a built-in calculator where you could list which ions are present in your buffer at what concentrations, and the software will calculate the ionic strength.
Are there any other difficulties faced when determining particle size?
There are times when the particles are too big to be measured by dynamic light scattering. In the Mobius instrument, the particle size can be measured up to five microns in radius. However, when the particle size exceeds this limit, an alternative technique can be used such as scanning electron microscope, tunneling electron microscope or atomic force microscope, to measure the particle size. This particle size can then be entered into the software which will use that radius to calculate the zeta potential.

What other aspects of the Mobius make it an ideal instrument for particle analysis?
Those who measure particle size and zeta potential are often also interested in the stability of their particles. One way to further study stability is to measure your particle size and zeta potential as the temperature is being ramped, or to hold the sample cell at a fixed temperature over a set amount of time.
In order to accurately calculate zeta potential, you need to know both the mobility and the radius simultaneously. This can be complicated because the size might constantly be changing as the temperature is being ramped.
In the Mobius instrument, we simultaneously measure DLS and PALS. This allows us to concurrently determine both the particle size and mobility of the sample, and calculate an accurate zeta potential across the whole temperature-ramp profile. The Mobius instrument has two different types of cells that it can simultaneously measure DLS and PALS. One is the dip cell, and the second is the flow cell.
Do you have any more advice on getting the most out of the Mobius?
I want to offer a few tips on method development for delicate samples. Some samples will begin to aggregate and increase in size when a voltage is applied. For these samples I recommend first injecting the sample and then measuring at different voltages, from zero to five or six volts. In each of these voltage ranges you should measure the sample five times, and quickly. For example, the DLS would be very short with one-second acquisitions, and you would do that five times. The PALS collection would have a total duration of five seconds, so both DPS and PALS are only five seconds. We do this five times, to see the reproducibility at each of those voltages. If the radius remains quite constant throughout all the voltages used you know that the sample is stable.
Looking at zeta potential as a function of voltage amplitude, you will see that it begins to stabilize at a certain voltage. This is the ideal voltage that you would want to apply for this sample.
Next, you can re-inject the sample and measure directly at that voltage to get the most accurate zeta potential without being compromised by previous measurements. Finally (an optional step), at that final voltage, you could further optimize the settings by changing the collection time. Rather than using five seconds you could collect that 10 seconds, 30 seconds and 60 seconds to see if that brings the five measurements closer together.
Where can our readers go to find out more?
To find out more please visit www.wyatt.com/Mobius
About Jason Lin

In Jason’s role at Wyatt he utilizes a variety of light scattering techniques to investigate samples for bio-pharmaceutical companies, chemical companies, academic centers and government research labs. Jason obtained his PhD from the University of California Santa Barbara's Department of Chemistry.
Disclaimer: The views expressed here are those of the interviewee and do not necessarily represent the views of AZoM.com Limited (T/A) AZoNetwork, the owner and operator of this website. This disclaimer forms part of the Terms and Conditions of use of this website.