Nanomechanical Measurement of the Strain-Stress Relation

Advanced design and manufacturing drive the need for nanomechanical testing because material properties depend on microstructures.

During material elastic deformation, the strain increases in proportion to the applied stress, with the constant of proportionality being the Young’s Modulus of the material, E. The onset of plasticity is identified as the yield point, or the point at which the strain begins to increase disproportionately to the stress. Beyond the yield point, a variety of microstructural mechanisms determine the relation between stress and strain; these include dislocation motion and entanglement, grain boundary sliding, micro-fracturing, etc.

Overview of Experimental Technique

The entire stress-strain curve can now be determined using nanoindentation with a flat-ended cylindrical punch and novel analysis of the resulting force-displacement data¹. Unlike pyramidal indenters, the flat-ended cylindrical punch imposes a changing strain on the test material, thus allowing the relationship between stress and strain to be probed. In contrast with spherical indenters, the maximum shear stress in the test material occurs at the surface (at the edge of contact) and so the onset of plastic yield is more easily detected. Because the contact radius is both known and constant, the strain can be increased without incorporating new material into the test. Unlike micropillar compression, this experimental technique requires no special sample preparation beyond what is normally done for nanoindentation. Finally, new analysis of flat-punch nanoindentation returns the stress-strain curve from the force-displacement data, which are normally acquired during nanoindentation testing.

Theory

KLA’s proprietary method for deducing the stress-strain graph from flat-punch nanoindentation readings requires an initial accurate adjustment of the indentation depth, h, to align with the uniaxial strain, ε. Subsequently, the average contact pressure, p_m, needs appropriate scaling to match the uniaxial stress, σ.

The determination of strain is executed by adjusting the indentation depth in the following manner:

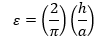Eq. 1

where a denotes the radius of the flat-ended punch. The stress is determined by scaling the mean pressure as the following:

where ζ is not a fixed number and is computed based on the degree of plasticity. The degree of plasticity is quantified by the parameter S^*, and is defined as:

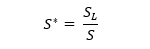Eq. 3

with S_L denoting the instantaneous slope of the loading curve, and S denoting the elastic contact stiffness.

In the limit of a completely elastic contact, due to the loading slope being equal to the contact stiffness, S^* takes the upper limit of unity. However, in the limit of a completely plastic contact, due to the unloading slope being infinite, S^* takes the lower limit of 0.

With dynamic nanoindentation, ζ is calculated throughout the loading cycle for utilization in Equation 2 and is defined as:

Here, the constants were defined by hundreds of finite-element simulations on a broad range of materials, giving the best agreement between the stress-strain curves attained by the approach and the stress-strain curves that were utilized as input to the simulations.

Measurement of Yield Stress-Strain for Titanium

Due to its formability and cost-effectiveness compared to its alloys, pure titanium is often selected for components that experience minimal external forces.² For pure titanium, the Young’s Modulus is approximately 120GPa.³ The onset of plastic deformation in titanium and other metals is marked by the yield point, the stage where the strain does not increase linearly with the stress. Past this point, multiple microstructural factors, such as dislocation movement and intertwining, grain boundary shifts, and microscopic fractures, influence the stress-strain relationship.

Given its microstructure, the yield strength of pure titanium can vary between 170 and 480 MPa.⁴ Pure titanium may be stronger when it is used in small volumes,⁵ and as a result, it may have new commercial applications.

Experimental Method 

Motivated by the objective of measuring yield strength and hardening at the microscopic scale, nanoindentation is employed to measure the stress-strain relation of pure titanium by using a flat-ended cylindrical punch with a diameter of 10 µm. The KLA Instruments iMicro nanoindenter was used with a flat-ended cone with a face diameter of 10 µm and an included angle of 90^o. Using the Flat Punch on Metals for Stress-Strain test method, the iMicro nanoindenter was employed to carry out 12 indentations on a prepared sample of commercially pure titanium.

The spacing between indentations was 75 μm, and the indenter was pushed into the surface at a constant displacement rate of 50 nm/second for each indentation to the maximum depth of 1600 nm.

A small oscillation of 2 nm at 110 Hz was added to the semi-static loading to assess the elastic contact stiffness during loading.

Initially, the Young’s modulus of the metal is needed as an input, sourced either from published literature or from earlier measurements using standard nanoindentation.

The theory for measuring strain and stress is not applicable until there is full contact between the flat punch and the surface. During the test, the point of full contact is defined when the below criteria are satisfied:

This is principally the stiffness relation determined by Sneddon.⁶

After this point, the stress-strain relation is calculated according to the Equations 1-4 detailed above. Beyond the point of full contact, these stress-strain ordered pairs are fit to the form of power-law hardening to acquire best-fit values for both K and n.

Points on the stress curve before full contact is achieved are determined according to Equation 1 and Equation 6 for strain and stress, respectively. The yield point is defined as the point of intersection between Equation 6 and the linear part of the stress-strain curve, which is set by the Young’s modulus value that is input.

Results and Discussion

Figure 1 displays the stress-strain curves for the 12 indentations. For all 12 tests, the yield stress was 270 ± 50 MPa, which agrees with the value of 240 MPa measured by the tensile test and reported by Kyocera,² and it is also well within the reported range of values by others.³

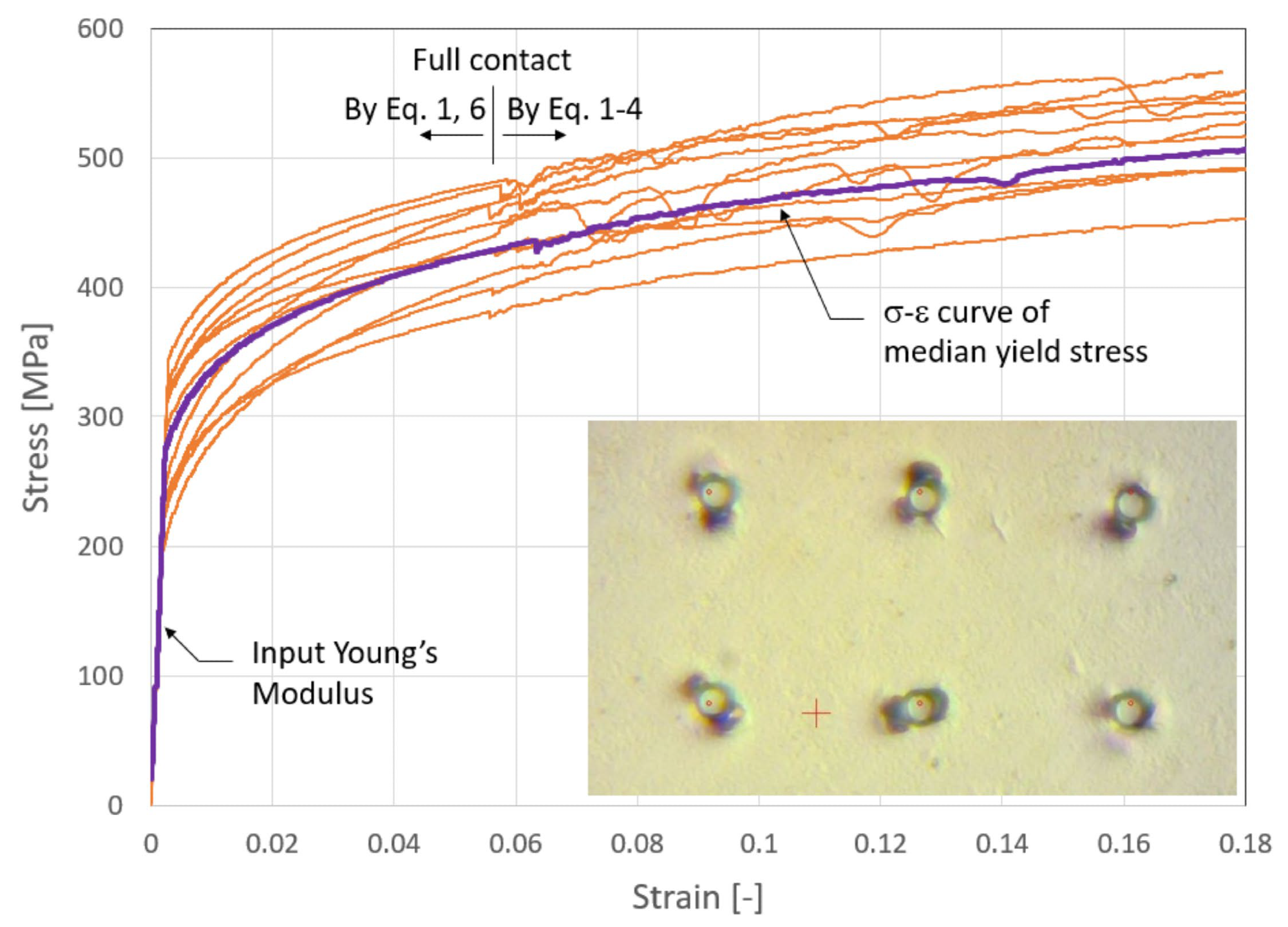
Figure 1. Stress-strain curves of pure titanium measured by 12 individual indentations with 10 μm flat-ended punch. Inset: Six residual impressions (75 μm spacing). Image Credit: KLA Instruments™

The scatter between tests may be greater than expected; this is due to each test being small enough to be confined to a single, randomly oriented grain. Many have attempted to use a spherical indenter to measure small-scale stress-strain curves, but limited success has been reported.⁷

Spherical indentation presents multiple challenges due to the uncertainty in the contact area generally being greater for spheres than for alternative indentation shapes. As the contact area increases, the volume of material being tested also increases, which gradually and continuously incorporates virgin material into the test. As a result, both the strain and the material are simultaneously changing.

With a flat punch, the contact area is well-known and fixed as the area of the punch face. Given that the contact area remains unchanged, the volume of the material tested stays approximately the same during the test.

Conclusion

Mechanical behavior and specifically the yield stress-strain relation at small scales may be influenced by material microstructure, microfracture, boundary dislocation and other local effects. The stress-strain relation of pure titanium at the micro-scale was measured by employing nanoindentation with a flat-ended punch, generating a measured yield stress of 270 ± 50 MPa. The KLA Instruments iMicro nanoindenter with the Flat Punch on Metals for Stress-Strain test method delivers a reliable technique for quantifying the yield stress for metals, alloys, and bulk metallic glasses (BMGs)⁸.

For more information and live demonstrations of nanoindentation and other metrology solutions from KLA Instruments, come visit us in person at Booth 503 at the Materials Research Society fall conference in Boston, Massachusetts, November 28-30, 2023. Bryan Crawford of KLA Instruments will present “See It, Feel It, Resist It: Flexible Metrology Solutions for Materials Research” at the Exhibitor Workshop, Tuesday, November 28, at 11:30 am. 

References

1. J. Hay, “Instrumented indentation apparatus having indenter punch with flat end surface and instrumented indentation method using the same,” US Patent US10288540B1, KLA Corporation, 2019.
2. H. Tada, “Manufacturing technologies for titanium eyeglass frames,” Titanium for Consumer Applications, Chapter 13, editors F. Froes, M. Qian, M. Niinomi, Elsevier, 2019: 235-268.
3. Kyocera, Titanium Properties, https://kyocera-sgstool.co.uk/titaniumresources/titanium-information-everything-you-need-to-know/titaniumproperties/, accessed March 9, 2020.
4. R. Osman and M. Swain, “A Critical Review of Dental Implant Materials with an Emphasis on Titanium versus Zirconia,” Materials (Basel) 2015: 8:932-958.
5. W. D. Nix and H. Gao, “Indentation size effects in crystalline materials: A law for strain gradient plasticity,” Journal of the Mechanics and Physics of Solids, 1998; 46(3):411-425.
6. I. N. Sneddon, “The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile, “ International Journal of Engineering Science, 1965.
7. E.G. Herbert, G.M. Pharr, W.C. Oliver, J.L. Hay and B.N. Lucas, “On the measurement of stress-strain curves by spherical indentation,” Thin Solid Films, 2001.
8. S. Zhang, X. Wang, J. Hay, U.D. Schwarz, A. Datye, "Mechanical-cycling induced evolution of structure and local mechanical properties in a PdCuNiP bulk metallic glass," Journal of Non-Crystalline Solids, 2024. 

More Content From KLA Instruments

Indentation University Session 22: Theory of Measuring Stress-Strain Curves by Nanoindentation

Indentation University Session 23: Nanoindentation for Stress-Strain

This information has been sourced, reviewed and adapted from materials provided by KLA Instruments™.

For more information on this source, please visit KLA Instruments™.