A defined experimental procedure is needed for DLS Microrheology characterization of a specific complex fluid type, in order to prevent the possible measurement pitfalls. This article outlines such a procedure and also provides examples of when it may be applied.
DLS Microrheology Methodology
The following sequential steps are recommended for characterizing a new sample type:
- Suitability of probe particle chemistry needs to be assessed to reduce particle-matrix interactions
- Zeta potential of probe particles are measured and compared first in the base solvent, and then in the sample
- Probe particle concentration is assessed for measurement in single scattering regime
- If the dispersion of the probe particles is proper, then some amount of probe particles is added to the sample
- Autocorrelation function (ACF) and intensity Particle Size Distribution (PSD) of resulting sample are measured
- Then ACF and Mean Square Displacement (MSD) of probe particles are measured to obtain Microrheology data for the sample being tested
- The Microrheology data is then checked for whether the data is independent of probe particle size and probe particle concentration
- Measurements are performed repeatedly at different probe concentrations and with different probe size (if possible)
- Microrheology measurement is then performed at two different probe particle concentrations higher than the values determined above to ensure whether the resulting MSD is independent of concentration
- Microrheology measurement is then performed with a larger probe size but with the same surface chemistry to ensure whether the resulting MSD is independent of probe particle size.
An autocorrelation function (ACF) measurement can only be performed after assessing a specific sample type for an appropriate probe particle type, concentration and size to obtain Microrheology data. At this point only the rheological testing of samples can be easily and rapidly performed with minimal volumes (below 20µl is possible).
Examples of DLS Microrheology
Measurements on an Ideal (Newtonian) Liquid
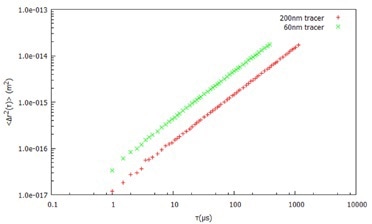
Figure 1. Mean Square Displacement (Δr2 (t)) with time for two different probe sizes in water.
Using DLS and dispersed probe (tracer) particles of known size, the viscosity of a Newtonian liquid can be directly obtained from the diffusion coefficient of the Stokes Einstein equation. In this example, water is measured using the full DLS Microrheology approach to demonstrate that there is no frequency dependence of the viscosity.
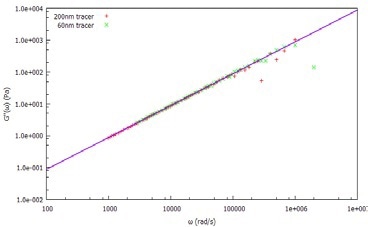
Figure 2. Viscous (loss) modulus, G", of water measured using 60nm and 20nm tracer particles.
After dispersing two probe (tracer) particle sizes (60 nm and 200 nm latex) in water, the MSD is determined (Figure 1) by measuring the ACF of the light scattered by both tracer sizes. From the MSD, the viscoelastic moduli are calculated, as shown in Figure 2.
Both tracer particles generate essentially the same results, demonstrating the frequency-independent behavior as anticipated from an ideal (Newtonian) liquid.
Polyethylene Oxide (PEO) Solution
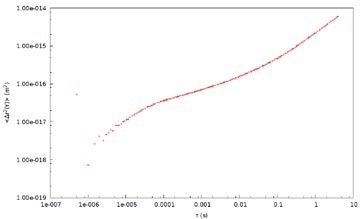
Figure 3. Mean Square Displacement (Δr2 (t)) with time for 700 nm tracer probes in 2% PEO solution.
DLS Microrheology data can be compared with Mechanical (Rotational) rheology using PEO solution as a ‘model system.’ Measurement data depicted in this example is acquired with 700 nm latex tracer particles in a 2% by weight solution of PEO in water (Figure 3). The MSD of the tracer particles in PEO is nonlinear with time, which is attributable to the viscoelasticity of the sample.
The MSD behavior is sub-diffusive at short timescales, indicative of an elastic modulus. The probe particles demonstrate ‘hindered’ motion at the shortest timescales. The MSD curve trends to a plateau at longer timescales and the elasticity of the system effectively traps the probe particles. Moreover, the probe particles can ‘escape’ when the material relaxes at the longest timescales.
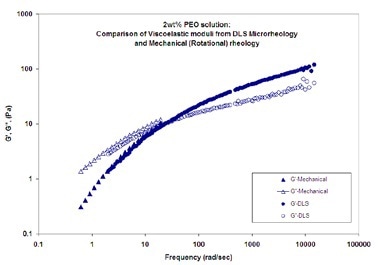
Figure 4. Viscoelastic moduli (elastic (storage) modulus, G', and viscous (loss) modulus, G'') as a function of frequency for a 2wt% PEO solution in water
DLS Microrheology and mechanical (rotational) rheology measurements of viscoelastic moduli (elastic (storage) modulus, G', and viscous (loss) modulus, G'') as a function of frequency for a 2wt% PEO solution in water are shown in Figure 4. The probe particles used are 700 nm latex. The results from the two techniques show good agreement.
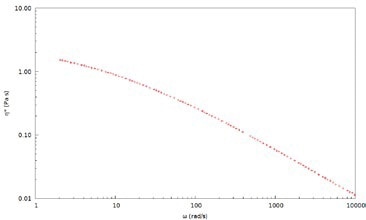
Figure 5. Complex viscosity, η*, for a 2wt% PEO solution in water measured with 700 nm latex tracer particles
DLS Microrheology extends the viscoelastic data to higher frequencies, thereby allowing for a more comprehensive characterization of rheological properties and dynamics of polymer solutions for a broad range of concentrations. This is not possible with mechanical rheology because of inertia limitations. Frequency-dependent viscosity demonstrates that the solution is non-Newtonian and exhibits shear thinning behavior. Complex viscosity, η*, for a 2wt% PEO solution in water measured using 700 nm latex tracer particles is depicted in Figure 5.
Protein Solutions
As DLS Microrheology extends the measurement range for polymer solutions, it can also be used for the characterization of protein solutions, which also show weak viscoelastic behavior on short timescale (high frequency) deformations. With small sample volume and low stress nature, the DLS Microrheology technique is advantageous, especially for protein solutions.
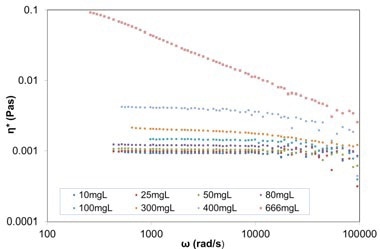
Figure 6. Plot of complex viscosity against frequency for varying concentration BSA in PBS solutions (from 10mg/ml up to 666mg/ml), from DLS Microrheology measurements (using 615nm carboxylated melamine probe particles).
Viscosity measurements of BSA solutions at different concentrations are provided here as an example. Plot of complex viscosity against frequency for different concentrations of BSA in phosphate buffered saline (PBS) solutions (from 10mg/ml up to 666mg/ml), from DLS Microrheology measurements utilizing 615 nm carboxylated melamine probe particles is depicted in Figure 6. The BSA solutions become non-Newtonian at concentrations above 80mg/ml, where the viscosity is no longer constant with frequency.
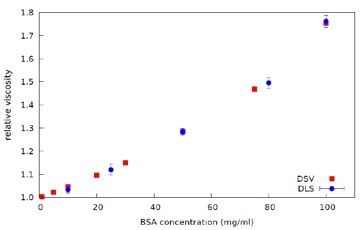
Figure 7. Plot of Relative Viscosity against Concentration for BSA in PBS solutions - data from DLS Microrheology (ref. Figure 4) and Dilute Solution Viscometer (DSV), at 25°C.
The complex viscosity data is then extrapolated to zero frequency to obtain Zero Shear Viscosity. The Relative Viscosity is then calculated from the ratio of the Zero Shear Viscosity for each BSA concentration to the viscosity of the PBS, as shown in Figure 7. Industrially relevant protein concentration range can be measured effectively and quickly using DLS Microrheology, with much smaller sample volumes when compared to other available methods.

This information has been sourced, reviewed and adapted from materials provided by Malvern Panalytical.
For more information on this source, please visit Malvern Panalytical.