The analysis of particulates in oils, including the type of particulate, its morphology and the amount as a function of size, encompasses the most direct means of any class of instrumentation with which to evaluate for machinery condition and contamination.
The population and size of wear particles increases when a machine enters an abnormal wear mode. When the wear surface stresses in a diesel engine become excessive due to load and/or speed, large severe sliding wear particles are produced.
The unique collection of particulate analysis tools from Spectro Scientific, headlined by the LaserNet Fines® (LNF) series, expands the scope of complete particulate analysis. The analysis toolbox is expanded to encompass systems from aerospace hydraulic systems, which may generate particulates measured in the single particles per 100 ml of oil to over-the-road truck engines, which may have millions of particles in a single ml of oil.
Particular emphasis is placed on providing information in addition to size-based counting, while ensuring the accuracy of the size-based counting.
Comprehensive particle analysis includes an assessment of the morphology of generated particulates, as provided in LNF and ferrography. Established by over 40 years of research in machinery breakdown, particle morphology can directly pinpoint the type of wear (wear mode) and provide a gauge of the severity of the component wear, while helping to find the generation source, including external contamination.
Finally, the most basic classification in particle analysis, whether the particles are a result of external contamination or wear, can be determined by measuring ferrous debris particulates in the oil.
Dynamic Equilibrium – Large Wear Particles in Oil Lubricated Systems
There are many approaches used to model a machine’s wear formation. Based on a balance between production rate and loss rate of particles in a machine, wear particles of different sizes reach their own dynamic equilibrium condition.
The result of this dynamic equilibrium model is the ability to predict, based on particle count trending information, what is a normal level and the level increase in particle production during the trend towards equilibrium, including at equilibrium, and what is abnormal for a given machine.
It is assumed that particle production follows a unique behavior per machine and is measured by the analytical instrumentation. For loss rate, it is assumed that there are various competing mechanisms to remove the particles during passage of oil through the system (Figure 1). These mechanisms are:
1) Filtration
2) Settling
3) Impaction and adhesion
4) Comminution (grinding up of particles)
5) Dissolution (oxidation or other chemical attack)
6) Magnetic separation

Figure 1. Simplified Machinery Oil Path.
In particular, the rate of increase in concentration of particles in a given size range is:

Where:
CL = Concentration of particles (mg/L)
PL = Production rate of particles (mg/h)
k = Removal Rate Constant (L/h)
V = Oil Volume (Liters)
t = time (h)
PL – kCL = net rate of addition of particles to the oil (mg/h)
Integrating from t=0 and CL = 0, and assuming a constant production rate provides the concentration of in a given size regime as a function of time:
| CL = PL/k(1-exp[-(k/V)t]) |
(1) |
The concentration reaches a steady value of PL/k once equilibrium is reached. If it is assumed that filtration is the only capture mechanism at work, and a capture efficiency of 1% for 4 - 10 µm particles given a 40 µm pleated filter cartridge and a constant flow rate of 7.5 liters/ min (450 liters/h) through the filter, then the removal rate constant for these particles can be calculated as:
| k = F*eff = 450*.01 = 4.5 L/h |
(2) |
Where F is the flow rate (liters/hr) and eff is the efficiency of the filter (0.01).
Then, the time to reach equilibrium for a given oil volume (Table 1, Figure 2) can be immediately calculated. When equilibrium is defined as the point at which the concentration of these particles reaches 99% of its equilibrium level, then, from Equations [1,2]:
| teq = -(V/k)*In(.01) = -(V/F*eff)*In(.01) = 1.02*V hours |
(3) |
The number of times that the oil has circulated before reaching equilibrium can be calculated as:
| #Cycles = teq*F/V = 1.02*F |
(4) |
Note that this is independent of volume.
Table 1. Time to equilibrium for different oil volumes assuming a 1% capture efficiency and 7.5 liter / min filter flow rate.
| 1% Capture Efficiency (4-10 micron particles) |
| Oil Volume Liters |
Flow Rate L/h |
# Cycles |
Total Volume (L) to equilibrium |
Time to reach equilibrium (hours) |
| 40 |
450 |
459 |
18360 |
40.8 |
| 20 |
450 |
459 |
9180 |
20.4 |
| 10 |
450 |
459 |
4590 |
10.2 |
| 5 |
450 |
459 |
2295 |
5.1 |
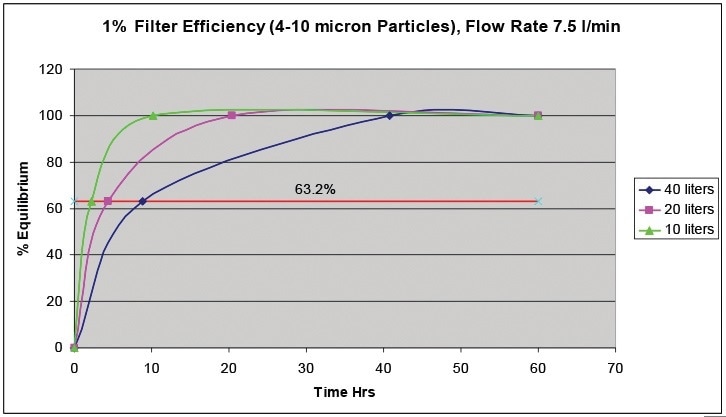
Figure 2. Time to equilibrium for 10, 20, and 40 liter sump capacities.
This simple diesel engine example shows that oil flow rate, oil volume capacity, particle size, and filtration efficiency will all have an impact on the time to equilibrium. As it governs when a sample should be taken either between an engine overhaul or routine oil change, the time to equilibrium is critical to the oil analyst.
This example shows that even for the biggest capacity engine, the time to equilibrium is relatively quick. However, in other applications where there are multiple loss and production mechanisms, it might take considerably longer.

This information has been sourced, reviewed and adapted from materials provided by AMETEK Spectro Scientific.
For more information on this source, please visit AMETEK Spectro Scientific.