Sponsored by AdmesyFeb 14 2018
Various optical systems or geometries can be used to perform light measurements. For instance, the total power [flux] of a light source can be measured in all directions, in a specific direction or for the light that falls upon a specific area.

Image Credit: Leigh Prather/Shutterstock.com
The necessary optical configuration of a measurement setup relies on the measured unit of power. Lenses, integrating spheres, and cosine correctors, which we will explore in this article, are the three most widely used optical configurations.
Optical Configurations
Integrating Sphere
An integrating sphere is basically a hollow spherical cavity covered with a diffuse, highly reflective white coating. This integrating sphere is mainly used to diffuse the radiation in all directions by scattering and reflecting the emitted light multiple times.
Spectroradiometers are generally coupled to integrating spheres to measure the characteristics and quantity of the light source being tested. Integrating spheres are available in a variety of sizes based on the construction, dimensions and power output of a light source.

Spectroradiometers can be connected to integrating spheres. Image Credit: Admesy
Cosine Corrector
A cosine corrector is a diffuse surface and is used to capture light upon a surface over a 180-degree angle. The surface of cosine correctors respond in accordance with Lambert’s cosine law: the amount of light falling upon the cosine corrector is proportional to the cosine of the light beam’s incident angle.
At a 60 degree angle, only half the intensity is measured as opposed to 100% at a 0-degree angle.

ASTERIA SERIES Compact, fast industrial light meter. Image Credit: Admesy
Lens
Lenses on measurement devices are typically used to observe a target area. The covered area captured by the lens relies on the acceptance angle and distance of the lens. Lens optics are generally used to measure homogeneous surfaces, for example, the backlights of displays.

HYPERION SERIES The next step in color measurement. Image Credit: Admesy
Measurement Principles
In addition to the optical configuration, the measurement principle used is also vital in light measurement.
The three main principles which express the power [flux] of a light source in a specific quantity are the photometric principle, the radiometric principle and the spectroradiometric principle.
Based on the measurement principle used, the power is expressed either according to the response of the human eye [photometric] in an absolute quantity [radiometric], or per wavelength [spectroradiometric].
These measurement principles are measured using spectrophotometers, radiometers and spectroradiometers, respectively. The following table gives a summary of these measurement principles and the optical configurations used to achieve specific light quantities.
The Spectroradiometric Principle provides all radiometric quantities per nanometer and is measured by means of a spectroradiometer. Radiant power for example is expressed in Watts, thus its spectroradiometric equivalent in Watt per nanometer.
The different optical configurations, in combination with the measurment principles, provide different measurements of light, each with different units, which can be viewed using the table below;
| Geometry |
|
Optical configuration |
Measurement principles |
| Radiometric |
Spectroradiometric |
Photometric |
| Power or flux |
Integrating Sphere |
Radiant Power
Watt, W |
Spectral Radiant Power
Watt per nanometer, W/nm |
Luminous Power
Lumen,
lm |
| Power/area |
Cosine Corrector
Integrating Sphere |
Irradiance
Watt per square meter, W/m² |
Spectral Irradiance
Watt per square meter per nanometer,
W/m²/nm |
Illuminance
Lumen per square meter, lm/m² = lux |
| Power/solid angle |
Cosine Corrector
Integrating Sphere |
Radiant Intensity
Watt per steradian, W/sr |
Spectral Radiant Intensity
Watt per steradian per nanometer, W/sr/nm |
Luminous intensity
Candela, lm/sr = cd |
| Power/area/ solid angle |
Collimating Lens |
Radiance
Watt per square meter per steradian, W/m²/sr |
Spectral radiance
Watt per square meter per steradian per nanometer, W/m²/sr/nm |
Luminance
Candela per square meter, Im/m²/sr = cd/m² = nit |
Radiometric

Image Credit: Admesy
The first principle [radiant flux or radiant power] refers to the total power emitted by a source in all directions.
During the development and production of lighting, radiant power measurements are quite common; the Watt: W is the unit of radiant power.
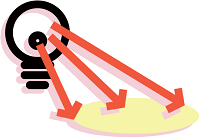
Image Credit: Admesy
Irradiance refers to the amount of radiant power incident on a surface and it is expressed in Watts per unit area: W/m2.
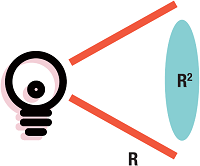
Image Credit: Admesy
A source’s radiant intensity is a directional quantity that defines the total amount of power emitted per solid angle. Therefore, radiant intensity is expressed in Watts per solid angle: W/sr.
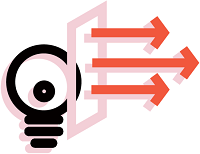
Image Credit: Admesy
Radiance is the fourth principle. It is the radiant intensity per unit projected area and defines the total amount of power per solid angle emitted from an area. It is expressed in Watts per unit area per solid angle: W/m2/sr.
Photometric
Unlike spectroradiometry and radiometry, the photometric principle measures light based on the response of the average human eye. This response is called the luminosity function Vλ.

Image Credit: Admesy
Luminous power is the photometric equivalent of radiant power and it is expressed in Lumens: lm. Typically, luminous power is measured using an integrating sphere, similar to its spectroradiometric equivalent.
Image Credit: Admesy
Illuminance is measured using light measurement devices integrated with cosine correctors. Values correspond to the amount of lumen per square meter: lm/m2, also referred to as lux.
Image Credit: Admesy
Luminous intensity is the photometric equivalent of radiant intensity and it is expressed in candela: cd. This unit is generally used to measure the brightness of directional light sources, for example, spotlights.
Image Credit: Admesy
The brightness of homogeneous surfaces like displays is specified using luminance. Luminance is often expressed in candela per square meter: cd/m2 which is equivalent to nit – the currently less used unit.

 Download Admesy's Guide to Light for More Information
Download Admesy's Guide to Light for More Information

This information has been sourced, reviewed and adapted from materials provided by Admesy.
For more information on this source, please visit Admesy.