Particle Size: What is it and Why is it Important?

To put it succinctly, particle size is diameter or radius. However, the type of diameter or radius is critical, and additionally, there are non-spherical particles. This article presents some ideas for people who are not experienced in particle sizing.

Length vs. Mass

For particle technologists, the only response is length. However, recently at a national biochemistry convention, a number of protein chemists continuously described the molecular weight of a globular protein, a relative molar mass, as the protein’s ‘size.’ The group was surprised upon realizing this, as they refer to the size of a globular protein using nanometers. Apart from these protein chemists, it is likely that when referring to particle size, length in nanometers will be meant.

To Be or Not to Be a Sphere

Across every three-dimensional particle, the sphere is the most critical in particle sizing by a lot. This is not due to most particles being spheres, despite many coming near to it (monoclonal antibodies, unaggregated latex, spherical micelles, oil-in-water and water-in-oil emulsions, liposomes, etc.). They are even closer if measurements are averaged over rotationally diffusing particles¹. Throughout the timescales of a lot of kinds of measurements, rotationally averaged sizes are being measured and as such, a sphere frequently signifies a rational approximation. If extremely irregular particles are broken down because of abrasion, lengthy ones are broken down into smaller ones and which get more globular instead of less. This is similar to wind and water action creating smooth, globular rocks from the rough shards of volcanic debris. It is also similar to irregular and/or rough particles rounded off as they are combined or stirred before becoming the final product.

Considering the 1^st law of thermodynamics, a liquid body without external forces will create a sphere to lessen its surface area for a particular volume of material. As such, liquid droplets, disregarding outside forces, form spheres. This is the reason that cooling planets created, to 1^st order, spherical objects.

The most critical reason might be that a lot of 2^nd-order differential equations that explain the physics of the automated techniques employed for measuring particle size are exactly soluble for spheres. This results in fitting nature into what can be achieved conveniently. One positive is that it usually works particularly for the purposes of quality control.

Image Credit: Brookhaven Instrument Corporation

A Quick Tour of Spherical Geometry

The volume can be 4 πr³/3 or πd³/6, where two times the radius r equals the diameter d. For completion, the surface area of a sphere can be 4 πr² or πd².

The simple factor of two that correlates radius to diameter is often the cause for a 100% error. If a requirement for size does not register it as radius or diameter, or if a result (mean size, for example) does not denote which it is, or a graph is not labeled, then the only option may be to guess. An assertion of ability to measure up to 5 microns in radius is the same as the assertion of 10 microns in diameter. This area should be considered as it happens fairly frequently and sometimes to deceive, particularly in advertising.

The Equivalent Spherical Diameter, ESD

There are two kinds, geometric equivalent and technique equivalent.

Geometric ESD’s

When considering a static, 2D image of a particle, it is not three dimensional. As such, what appears like a circle may correspond to a thin disc-like particle rather than a sphere if shadows do not show a more structure that fills more space. When the image was taken, as long as it was not a 3D holographic image, it could be thought that as the particles settle, they become steady on a flat surface. As such, if they did not land on their faces, most discs would topple over if they landed on an edge.

There are a lot of variously geometrically defined ESD’s that might be assigned to an irregular particle. A way to ascertain the ESD of an arbitrarily shaped particle is to draw circles around the actual image until it is just simply totally enclosed. The diameter of the enclosing circle should be assigned to that of the particle (d_e).

Instead, it is possible to identify a circle with an area equal to that of the measured particle area. This can be carried out simply by counting pixels and computer programs that cause constantly growing accuracy with smaller and smaller pixels. With the area of the drawn circle, its diameter should be assigned to that of the particle (πd²/4). This ESD should be labeled dA. Alternatively, the image’s perimeter could be traced and assigned to the diameter of the circle with the like perimeter (πd_P).

Each of these is a geometric equivalent diameter. There are many more options based on parallel tangents (Feret’s diameter, d_F) and chords (Martin’s diameter, d_M). The fact that the same particle may have numerous kinds of geometric ESD’s should be noted, and if correctly identified, they should not be equal with a more irregular particle shape. The ratio of two of these geometric ESD’s for the same particle shows something regarding shape and space filling.

It becomes more difficult to describe the particle shape with just one parameter, the more irregular it becomes. Due to this, the understanding of ‘size’ established by image analysis is more challenging than an automated machine centered on an ESD defined by the method. What is implied by this kind of ESD?

Technique ESDs

When considering a stack of sieve plates, the mass of all the particles that stay on a specific plate (following suitable shaking) whose hole size² is d_S are known to signify the collective increment by mass bigger than diameter d_S. When considering a particle falling under gravity or moving radially outward in a centrifuge, its velocity is calculated and then set equal to that of a sphere that would have shifted in the same way.

The consequent diameter is known as the Stokes diameter, d_St, due to the motion being described by Stokes Law. If a rotating, tumbling particle’s diffraction pattern is recorded on a detector, then the pattern is set equal to that of a sphere that would provide the nearest diffraction pattern.

This is known as the laser or laser diffraction particle size and should be labeled d_LD. Employing dynamic light scattering to ascertain the translational diffusion coefficient of a submicron particle should be considered. Then the hydrodynamic diameter or radius relating to the measured diffusion coefficient needs to be calculated. This should include two subscripts: H for hydrodynamic and DLS for the method (d_{H, DLS}). Double subscripts such as this are not usually seen in practice; however, if they were, it would be increasingly apparent what was measured.

In each of these cases and a lot more, the size of the sphere is designated such that it would provide the same outcome as the actual particle. These are known as technique ESD’s (or ESR’s). However, what could be observed in practice is either d or r and this causes confusion when assessing outcomes. For spheres, if methods were equally accurate, then a subscript would not be required. However, for irregular shapes, employing subscripts, one would acknowledge that the ‘sizes’ should not be equal. As with geometric ESD’s, ratios of technique ESD’s generate information on shape.

There is just one definition for a given method (disregarding specialized flow orientation methods), unlike with image analysis. There lies the vulnerability of image evaluation: Which ones to select to portray the particle size? No universally applicable, simple standards to refer to exist.

The Promise and Heart Break of Image Analysis

For extremely long rods, the aspect ratio, AR, is known as the length divided by the diameter, L/d, and often the reciprocal is known as the AR. For further irregular particles, the most lengthy dimension separated by the shortest dimension is the aspect ratio, or its reciprocal is. Like the L and d for every particle in a distribution, the aspect ratio may be determined. A particle’s performance may be correlated with L, d, or possibly with AR. There are just three options here.

But imagine a more highly irregular particle, smooth or jagged. There are a lot of potential statistical descriptors of shape and size. Most modern software provides many options that can be employed, which can cause a problem.

It is important to ascertain which size parameter or subset of size parameters will correlate with particle performance? In some disciplines, outcomes are known; however, in many, they are not. Image analysis leads to large amounts of data, but it does not always lead to useful information.

There are further issues with image analysis, which are addressed in more detail in another s ‘A Guide to Choosing a Particle Sizer.’

Three Kinds of Radii

The first is the most well-known, which is the hard sphere, geometric radius, R_s. This radius is especially easily acquired employing image analysis.

Secondly, as previously described, in dynamic light scattering (DLS), the hydrodynamic radius, R_h is obtained. This radius is the one that is obtained from contrasting a sphere with the translational diffusion coefficient, which is measured. This is a solid, hard-core particle whose surface is covered with long-chain polymers or surfactants that stick far out into the liquid.

Often known as ‘hairy’ particles, their radii are substantially bigger than that of their cores. Finally, there is the radius of gyration, R_g, found from static light scattering (SLS). It is worth noting that the R_g obtained from SLS measurements is independent of shape assumptions; however, any R_h value assumes a sphere.

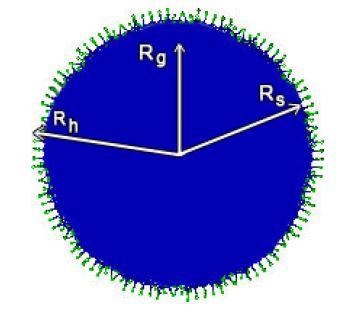
Image Credit: Brookhaven Instrument Corporation

Summary

After initially verifying that particle size is actually a length and not the mass of a protein, ascertain if the outcomes are pertaining to a single statistical parameter or are many parameters included utilizing image analysis. If it is a single statistical parameter, is it a true diameter or an ESD established geometrically (image analysis) or by contrast against what a sphere would produce employing an automated method (laser diffraction, centrifugation, sieving, zone counters, etc.). And, finally, it should be determined whether it is a radius or a diameter (a true one or ESD/ESR) being discussed. Answering these questions will establish an enhanced position to compare numerical outcomes more efficiently.

Footnotes

¹ The rotational diffusion coefficient, D_R, for a sphere of radius 1 micron in the water at 25 ºC is 0.18 s^-1 and it varies inversely with the cube of the radius. Thus, a 100 nm radius particle is diffusing (rotating) 180 times per second. If the measurement time is a second or longer, the results are rotationally averaged.

² Sieve sizes are a complete topic in themselves. Often, they are not circular holes. Abraded holes, as well as particles broken by abrasion, may be problems. Sifting long enough to ensure all smaller particles made it through is an issue. Finally, for highly irregular shapes, if the particle can be oriented by sifting, then it is the smaller dimension that is determined. Think of the distribution of long rods of varying lengths and varying, but much smaller, diameters. Although unlikely, you would be determining the size distribution of the rod diameters and learn nothing about the distribution of rod lengths if you could sift them such that they all stood on end when passing through the sieves’ holes.

Acknowledgments

Adapted from sources originally authored by Bruce Weiner.

This information has been sourced, reviewed and adapted from materials provided by Brookhaven Instrument Corporation.

For more information on this source, please visit Brookhaven Instrument Corporation.