Hyaluronic acid (HA), a naturally occurring, unbranched polysaccharide, has been the subject of intense research for its potential use in cosmetic, pharmacological, medical, and ophthalmic applications. The physiochemical behavior of HA relies on material characteristics, including molecular conformation, intrinsic viscosity ([η]), weight-average molecular weight (Mw), and molecular weight distribution or polydispersity index (PDI).
The Mendichi group at the Istituto di Chimica delle Macromolecole (Milan, Italy) has carried out many analyses involving on-line SEC of HA using MALS, single-capillary viscometry and concentration detection.
The unique combination of these detectors determines not only all of the abovementioned material characteristics, but also analyzes sample intrinsic viscosity and molecular conformation information by using the Mark–Houwink–Sakurada (MHS) relationship. This article presents on-line absolute characterization of HA properties by means of MALS, differential refractometry, and differential viscometry detectors in series.
Instrumentation
This analysis involved seven separate HA samples from different sources, Ovalbumin from Sigma, and all other required chemicals of analytical grade. The chromatographic system included a HPLC system, an autoinjector (Agilent 1100, 900-µL injection loop), and a solvent degasser (ERC L761).
The SEC column system comprised a Polymer Labs Aquagel – OH (8 µm) separation column with guard column. Phosphate-buffered saline (PBS, 8 mM dibasic sodium phosphate, 22 mM monobasic sodium phosphate, 150 mM sodium chloride in MilliQ-grade water) was the mobile phases, and the flow rate was 0.5 mL/min.
Chromatographic detectors used in series were a DAWN EOS MALS device, a ViscoStar differential viscometer, and an Optilab rEX differential diffractometer, all from Wyatt Technology. The MALS detector helps perform the absolute molar mass calculation without the requirement for column calibration, reference standards, or ‘fudge factors.’
The differential viscometer employs the conventional four-arm capillary bridge design, as shown in Figure 1. The bridge is consisted of four equal-impedance capillaries with the lower-left arm possessing an effectively zero-impedance delay volume.
The bridge can tolerate moderate pump pulses, thanks to its inherently insensitive design to pressure fluctuations. Moreover, the device is equipped with a Peltier thermoelectric device for accurate thermal control within a broader temperature range. The unique combination of modern electronics, precise thermal control, and bridge design yields a device with great S/N.
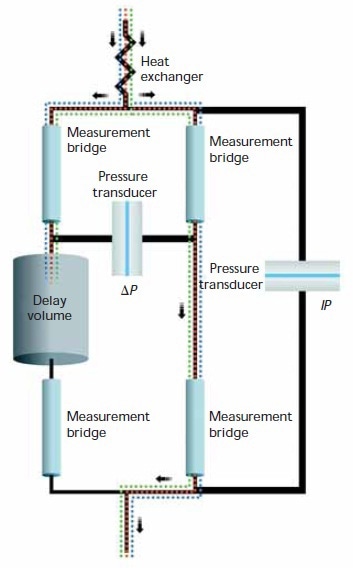
Figure 1. Schematic of the differential viscometer design.
Concentration measurements were performed using the differential refractometer. Accurate thermal control by means of a Peltier device enables thermal stability at or below room temperature, resulting in a device with stable baselines and very high S/N.
The concentration (c) value obtained from the differential refractometer and the ηsp value obtained from the differential viscometer enables the direct calculations of sample intrinsic viscosity by using the MHS relationship to every data piece throughout an elution peak. The inclusion of a light-scattering device makes the data fit to the MHS equation. The MHS relationship is,
[η] = K Ma
Where, M = molecular weight; ‘K’ and ‘a’ = MHS coefficients.
These MHS coefficients are measures of solvent interaction and polymer shape. The hydrodynamic volume Vh of the sample can also be calculated using the Einstein-Simha relation:
Vh = M [η]/(2.5NA)
Where, NA is Avogadro’s number. The hydrodynamic radius rh can be calculated from Vh by means of the following equation:
rh = (3Vh/4π )
The ASTRA V software package from Wyatt Technology was used to perform experimental collection and data analysis. This software allowed the collection and subsequent analysis of all 18 MALS angles along with the AP, IP, and differential refractometry signals.
Experimental Procedure and Results
It is necessary to determine the exact system constants specific to the experimental set-up prior to carrying out HA chromatographic analysis.
The differential viscometer needs to be placed upstream of the differential refractometer because the baseline behavior of the differential refractometer is susceptible to backpressure effects. Hence, the last detector must be the refractometer in the chromatographic flow path for the best S/N. A summary of material characteristics for the seven HA samples is provided in the following table:
Table 1. Summary of HA sample material characteristics.
| HA Sample |
HA Source |
Mw (g/mol) |
PDI |
Rg (nm) |
[η] (mL/g) |
rh (nm) |
| HA-1 |
Bacterial fermentation |
2.64E+05 |
1.19 |
57.7 |
632 |
27.7 |
| HA-2 |
Umbilical cord |
2.84E+05 |
1.23 |
66.1 |
652 |
28.3 |
| HA-3 |
Chicken comb |
6.62E+05 |
1.10 |
109.1 |
1431 |
51.1 |
| HA-4 |
Bacterial fermentation |
1.10E+06 |
1.45 |
165.4 |
1754 |
57.7 |
| HA-5 |
Umbilical cord |
1.44E+06 |
1.06 |
180.4 |
2208 |
77.7 |
| HA-6 |
Chicken comb |
1.62E+06 |
1.06 |
182.4 |
2671 |
86.1 |
| HA-7 |
"Natural sources" |
1.76E+06 |
1.02 |
207.9 |
2655 |
89.9 |
All solution concentrations were 0.1 mg/mL HA in PBS and the injection volume was 900 mL. The dn/dc value for HA, 0.167 (mL/g) was obtained from the literature. The selection of the low concentration and large injected volume was to prevent potential viscous-fingering of HA samples within the separation column. Results were in line with literature values. For each sample, injections were carried out multiple times to verify repeatability of the results.
A typical ηsp chromatogram of an HA sample together with corresponding Mw, Rg, and rh values throughout the peak is illustrated in Figure 2. The typical differential viscometer S/N of the trace for these HA analyses was in the order of 2200:1, one order of magnitude better than that of pulse-free, data-filtered single-capillary viscometry.
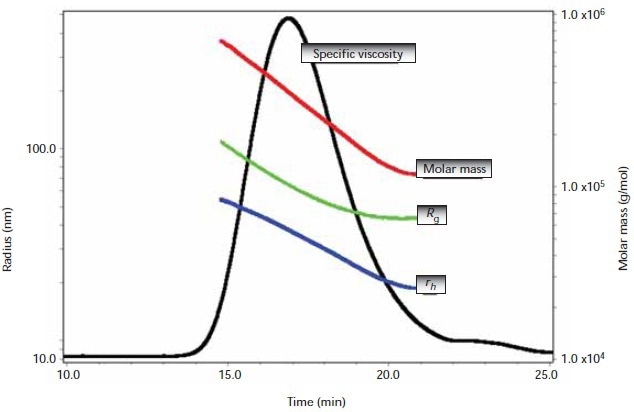
Figure 2. A typical ηsp chromatogram of an HA sample together with associated Mw, Rg, and rh values across the peak.
MHS plots have been created for all samples to assess molecular conformation information. A representative MHS plot of sample HA-2 is shown in Figure 3. It is also possible to observe the least-squares regression of the MHS trace in Figure 3. Although not presented in this article, all seven HA samples showed MHS curvature analogous to that depicted in Figure 3.
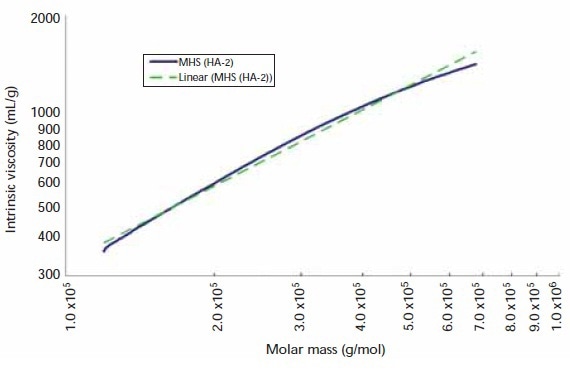
Figure 3. Mark–Houwink–Sakurada plot and linear fit for sample HA-2.
ai values of sample HA-2 shown in Figure 4 range from 1.0 at lower molecular weights declining to nearly 0.55 at high molecular weights. The six other HA samples demonstrated ai behavior similar to that of HA-2, with typical ai values ranging from 1.1 at low molecular weights to 0.5 at high molecular weights.
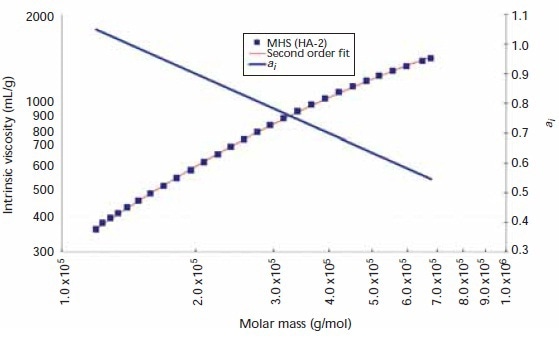
Figure 4. Mark–Houwink–Sakurada plot, second-order fit, and ai versus log (Mw) for sample HA-2.
This behavior is in good agreement with the theory that HA demonstrates free-draining, non-Gaussian chain behavior at lower molecular weights. The inherent stiffness of this polyelectrolyte drives the molecule to assume a more extended conformation at lower molecular weights, resulting in a corresponding high ai value. And when there is an increase in the molecular weight, ai values drop due to the transformation of HA into Gaussian chain behavior. This might help describe the broad range of HA MHS constants published in the literature.
Conclusion
The results show that the combination of a MALS instrument, a differential viscometer, and a differential refractometer with SEC is an ideal set-up to explore the material characteristics of the biopolymer HA, including the absolute molecular weight, radii information, and molecular weight distribution. The measured values are in good agreement with historical literature values.
The use of these detectors in conjunction with the software resulted in a rapid, precise, and absolute analysis of HA properties with unprecedented S/N and without the requirement for calibration curves for any of the detectors.

This information has been sourced, reviewed and adapted from materials provided by Wyatt Technology.
For more information on this source, please visit Wyatt Technology.