|
Since then, magnetostrictive TERFENOL-D has been commercially developed as the lanthanide material best suited to drive maximum acoustic power, relatively low-frequency equipment, including sonar.
TERFENOL-D is an intermetallic alloy of the lanthanide elements terbium and dysprosium combined with iron (Fe) and commercially produced as a near-single crystal. The name combines the symbols for the elements with NOL, derived from the facility of origin. The material is usually supplied to manufacturers ready to assemble into devices, without the need for further processing.
Design data now available enables the acoustic engineer to choose from the various possible sonar drive materials to produce a design which will best meet system requirements. Certain materials allow electrical and electromagnetic energy to conveniently be transduced (converted) into other forms of energy, such as mechanical energy. Transduction materials generally also show the opposite effect: conversion of incident mechanical energy into electromagnetic energy. While many materials function well as sensors, far fewer efficiently convert input electromagnetic energy into sizeable amounts of mechanical output energy.
Comparing Materials by Coupling Co-efficient
The most direct way to compare the various transduction materials is through a parameter symbolised k2 the square of the coupling coefficient. k2 measures the amount of incident energy transduced into output. To understand the physical origin and meaning of k2, consider the relatively well known analysis of an electrical transformer. The k2 parameter is a measure of the mutual coupling between two transformer coils. Here, the amount of magnetic flux generated by a coil of self-inductance L1 is related by the mutual inductance (symbolised as M), to the amount of flux threading through or linking a second coil of self-inductance L2. For any two coils, M has the same absolute value regardless of which coil is energised. Through an energy argument, the parameter k2 is defined as M2/L1L2, a ratio that represents the amount of an energy-coupling ratio. It defines the upper limit of incident electromagnetic energy converted into mechanical output energy. Excluding the inevitable losses, the rest of the incident energy is stored either as an electric field or a magnetic field, both of which can be recovered. If there is no coupling, k2 is zero and thermodynamics dictates that the upper limit can never exceed unity.
The strain of magnetostrictive materials tends to be quadratic. That is, regardless of magnetic-field polarity, they either constrict with increasing field (nickel) or expand with increasing field (TERFENOL-D). Quadratic strain is also a feature of a late-model ceramic known as PMN, for lead magnesium niobate. (Because strain is quadratic, PMN is correctly categorised as electrostrictive rather than piezoelectric). To maximise equal strain output around a null point, quadratic materials are partially expanded with a static field to the desired null.
This is known as bias. The alternating energy coupled between the two coils by a magnetic field. Using the same derivation method, it can be shown that M is equivalent to intrinsic material property d33 through which a bar of transducing material connects an axial electromagnetic field to an axial elastic field. The units of d33 are the axial strain in meters per meter divided by the incident field intensity in either amperes per meter or volts per meter. Similarly, L1 is equivalent to either the axial electrical permittivity ε33T or magnetic permeability µ33T where elastic stress T is held constant, and L2 is equivalent to axial elastic compliance 1/Y33X where incident electromagnetic field X is held constant. Then k2 is defined as:
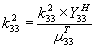
Magnetostrictive
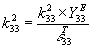
Piezoelectric
The subscript 33 means that cause and effect are both measured along the axial (3) direction.
Parameter k2 is sometimes referred to as energy efficiency, but it is really electromagnetic field superposed on the static field then enables positive and negative motion about the null. The common piezoelectric ceramic, PZT, does not need field bias for part of its range, but output can be maximised with bias. TERFENOL-D, PZT, and PMN couple more energy per unit volume if mechanical compressive stress bias (pre-stress) is maximised, with a corresponding electromagnetic-field bias. This is because larger stress excursions around null can be accommodated without overcoming the stress bias.
Conveniently, the U.S. Navy has compared very late-model PZT-8 and PMN data with TERFENOL-D. These data are reproduced in the table. The table is expressed in coherent MKSA SI units, permitting direct comparison of all electrical, magnetic, and mechanical quantities without need of multiplication factors. For historical context and reference, some properties of A-nickel, one of the better nickel magnetostrictive alloys employed in World War II Navy sonars are included in the table.
Thermal properties are from manufacturers’ published data. The Navy reference compares the electromechanical energy density limited both by field and by stress. These values are compared in the table.
Depoling
The tabulated properties do not show that the PZT data are taken near its long-life stress limit. That is, the PZT is not compressed further to avoid losing its performance. Because the piezoelectric phenomenon requires altering the natural crystal symmetry, piezoelectric ceramic performance continuously degrades as it tends to return to its natural state, a process known as depoling. Depoling is accelerated by any combination of overstress, overstrain, over-voltage, or over-temperature. Rates of depoling can be found for various commercial piezoelectric ceramics in manufacturers’ tables. It is assumed that the Navy operates its PZT sonar projectors at the maximum long-term stress limit to maximise energy transduction per unit volume of material and per unit of economical life.
Note that degraded PZT can be repoled to restore performance. As a matter of practicality and convenience, this is not typically done in installed equipment. Magnetostriction of aligned (near-single crystal) TERFENOL-D is an inherent property, and poling is not required.
Table 1. Comparison of Shape Change Material Properties
|
|
|
Mass Density
|
kg/m3
|
|
8900
|
7600
|
7800
|
9210
|
|
Elastic Modulus (Y33H)
|
N/m2
|
|
210x109
|
|
|
29x109
|
|
Elastic Modulus (Y33E)
|
N/m2
|
|
|
74.1x109
|
78.7x109
|
|
|
Permeability (µ33T)
|
V-s/A-m
|
|
75.4x10-6
|
|
|
5.404x10-6
|
|
Permeability (e33T)
|
A-s/V-m
|
|
|
8.854x10-9
|
115.1x10-9
|
|
|
Strain Coeff (d33)
|
m/A
|
|
-6.06x10-9
|
|
|
9.10x10-9
|
|
Strain Coeff (d33)
|
m/V
|
|
|
0.225x10-9
|
0.515x10-9
|
|
|
Energy Coupling (k332)
|
|
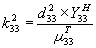
|
0.012
|
|
|
0.444
|
|
Energy Coupling (k332)
|
|
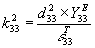
|
|
0.424
|
0.181
|
|
|
Prestress
|
N/m2
|
|
7x106
|
-41x106
|
-41x106
|
-41x106
|
|
Alternating Stress (Trms)
|
N/m2
|
|
4.95x106
|
29x106
|
29x106
|
29x106
|
|
Stress-Ltd Energy Density
|
J/m3
|
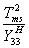
|
117
|
|
|
29000
|
|
Stress-Ltd Energy Density
|
J/m3
|
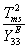
|
|
11300
|
10700
|
|
|
Field Bias
|
A/m
|
|
|
|
|
0.1x106
|
|
Field Bias
|
V/m
|
|
|
0
|
1x106
|
|
|
Alternating Field (Hrms)
|
A/m
|
|
8000
|
|
|
45000
|
|
Alternating Field (Erms)
|
V/m
|
|
|
390000
|
620000
|
|
|
Field-Ltd Energy Density
|
J/m3
|
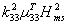
|
494
|
|
|
4912
|
|
Field-Ltd Energy Density
|
J/m3
|
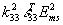
|
|
569
|
7801
|
|
|
Electrical Resistivity
|
|
|
68x10-9
|
>108
|
(high)
|
580x10-9
|
|
Thermal Conductivity
|
W/m-K
|
|
92
|
~2
|
~2
|
13.5
|
Definitions
µ0=4πx10-7 Volt-Seconds/Ampere-Meter is the permeability of free space.
ε0=c-2µ0-1 Ampere-Seconds/Volt-Meter is the permittivity of free space.
C=299,792,456 meters/second is the speed of light.
Units: A = ampere; kg = kilogram; m = meter; J = joules; K = degrees Kelvin; N = Newton; s = seconds; V = volt; W = watt.
The only known permanent degradation mechanisms of TERFENOL-D are melting, which requires temperatures greater than 1200°C, or mechanical shock. If not melted, cooling restores full performance. The limit of destruction is usually determined by the thermal limit of the solenoid coil used to impose the oscillating magnetic field.
Overstrain
TERFENOL-D cannot be overstrained. Manufacturers of commercial TERFENOL-D sonar claim tens of millions of cycles without measurable change. A Navy prototype TERFENOL-D driven projector is reported to have operated over 100 million cycles without failure.
When overstressed, TERFENOL-D output merely drops below the design value. Therefore, pre-stress can be increased beyond the tabulated values, maximizing device energy density. Magnetostriction is significant, near 70 MPa pre-stress, above which test data is limited. The ultimate tensile stress of piezoelectric ceramics is near that of TERFENOL-D, implying no advantage for either material with respect to mechanical shock sensitivity.
Electrical Conductivity and Eddy Currents
TERFENOL-D’s electrical conductivity combined with the changing magnetic field it transduces gives rise to eddy currents, which are not a consideration in ceramics. The effect of eddy currents in TERFENOL-D is minimised by lamination. The material is sliced parallel to its cylindrical axis (that is, parallel to its strain axis in contrast to a piezoelectric ceramic being cut perpendicular to its strain axis) and then bonded with an insulating epoxy. Recently, wire-saw techniques have been introduced in production, which minimise material loss and cost. It should be noted that all parts of the magnetic circuit must be designed for eddy current control.
Voltage Sensitivity
TERFENOL-D is not sensitive to voltage. For piezoelectric ceramic devices to be operated within reasonable voltage limits, the length of an individual element is limited. PZT requires an rms (root mean square) electric-field intensity of about 390 volts per millimeter thickness. (PMN is even higher.) Higher voltage shortens life. Extracting the power potential from PZT requires finite individual element thickness, dictated by electrical safety and practicality, including prevention of corona discharge. Displacement is attained by stacking individual pieces separated by a dielectric material. Stacking and wiring thin wafers imposes manufacturing and reliability problems. The compliance of the epoxy used to bond the wafers absorbs measurable output.
Piezoelectric ceramic electrodes are made of relatively precious materials such as silver and palladium. Inhomogeneous electric-field distribution gives rise to stress concentrations, resulting in micro-cracks and inactive areas near the electrode ends. Migration of electrode material into the ceramic may exacerbate voltage stress and micro-cracking.
Permittivity
On the other hand, piezoelectric ceramics exhibit a much higher relative permittivity with respect to free space than does the relative permeability of TERFENOL-D with respect to free space. This eases the task of ensuring electric-field uniformity contrasted with the task of ensuring magnetic-field uniformity.
Resonant Frequency
Successful design of an electromechanical transducer requires careful attention to dynamic system behavior at different frequencies and often at resonance. Employing a simplified lumped parameter approach, the undamped resonant frequency ƒn of an elastic bar of shape-change material driving a mass is approximated as the square root of stiffness divided by one third of its uniformly distributed mass plus the driven mass. An undamped system excited at resonance would self-destruct as energy was added to it with no other place to go. In the real world, there is always damping since all transduction materials operate irreversibly. Each material incorporates various damping mechanisms, which ultimately convert the motion into heat, and reduce the frequency of the theoretical undamped resonance to the real-world damped resonance. Additionally, ceramics inherently are poor conductors of heat. Heat buildup degrades performance, in come cases permanently.
Quality Factor
These dynamic behaviors can be summarised by Q, a parameter called the quality factor. Mechanical Q is a numeric measure of either the mass reactance divided by the damping resistance or, equivalently, it is the stiffness reactance divided by the damping resistance. Mass multiplied by circular frequency is called the mass reactance and assumes the same units as resistance, namely force per unit velocity. Similarly, spring stiffness divided by circular frequency is called the stiffness reactance. A material without losses would have a Q of infinity.
This simplified discussion of Q serves to illustrate its meaning in a purely mechanical dynamic system. There is an equivalent argument for a purely electrical dynamic system. However, in the case of transducing materials, particularly those with high electro-mechanical k2 coupling ratios, the transducer cannot be viewed in either purely electrical or purely mechanical terms. That is, when operated dynamically, the effects of the mechanical load are evident on the electrical side in the form of impedance changes, and vice versa. It is a common misconception to separate these effects, with consequent difficulties in understanding transducer dynamic behavior. Thus, the output stage of the electrical power amplifier and the load dynamics must be considered as a complete dynamic system during the design process.
Future Development Potential
Piezoelectric ceramics have enjoyed a long period of development funding and ingenuity to reach their near maximum potential as presented in Table 1. By contrast, the nominal properties of TERFENOL-D easily compare with the mature ceramics and exceed their development potential. Innovative TERFENOL-D transducer designs are still emerging, and full potential of the material has not yet been fully exploited in commercial designs.
Since the initial discovery of lanthanide magnetostriction, improved TERFENOL-D materials, design data, and models have become available to designers of sonar and other acoustic devices. Higher volume production and investment in improved manufacturing methods have resulted in a rapid decline in the costs of production TERFENOL-D.
Understanding the relative strengths of each material will aid the engineering designer in making the best choices for a given application.
|