Introduction The use of ultrasound as a tool in material science is increasing. The effect of ultrasound on organic synthesis, polymer reaction, electroplating, electrosynthesis and electropolymerization has been exploited to good effect [1]. Studies of ultrasonic irradiation show that it can be used for degradation of polymers. The breakage of chemical bonds is due to cavitation into the medium. Cavitation is the formation and violent collapse of small bubbles. This leads to shearing forces of sufficient magnitude to cause the rupture of chemical bonds [2]. Many researchers have investigated the ultrasonic degradation of polymers, as summarized by Price [2]. The effects of various parameters like temperature, ultrasound intensity, solution vapour pressure, frequency of ultrasonic waves and polymer concentration have been investigated [2, 3]. However, up to now, no report on the ultrasonic degradation of (Chlorinated Polypropylene) CPP has been seen. Chlorinated polypropylene has excellent abrasion resistance, age resistance and acid and alkali resistance. It also has excellent adhesion to polyolefin. As an adhesion promoter, CPP is widely used in polyolefin coatings, agglutinants, printing ink and compatibility assistants etc .In recent years, people have attached more importance to the study of CPP with rapid development of polyolefin [4]. In order to expand the investigation field of CPP, our research on the ultrasonic degradation of CPP in toluene solution is described in this paper. To determine the kinetic equation is an important basic work of study on ultrasonic degradation. The objective of this work has been accurately to determine the kinetic equation of CPP in toluene solution under ultrasonic irradiation. Experimental Materials and Equipment Chlorinated polypropylene (CPP), which contains 30% chlorine by weight, is a commercial product purchased from Jin Zhujiang Chemical Factory in Guangdong (China). The viscosity-average molecular weight of CPP is 174000 g/mol. Toluene is of A.R.grade. Ultrasonic irradiation was carried out using a JY92-II cell disintegrator made by NingBo(China) XinZhi Biochemical Controlled Limited Company operating at 68% of its full intensity, which is 650 W nominally at 20-25 KHz. The ultrasonic probe with a flat surface of 6mm in diameter contacts directly the sample solution. The reactor is a 450 ml glass vessel with a jacket to keep the temperature constant at 200C during the sonication. The volume of the sample solution is 240 ml. After a defined sonication period, a portion of sample solution is removed to measure its intrinsic viscosity [η] by Obblehode Viscometry. The experimental methods of research were improved as follows: (1) In previous literature, concentrations of polymers were usually below 5%(w/w)[5-8]. With industrial production in mind, we set the maximum concentration of CPP at 20%. (2) Ultrasonic time did not exceed 400 minutes in previous literature[5, 6, 9, 10, 12]. In order to investigate in detail the effect of the ultrasound time on molecular weight, in our study, we set the longest time at 3120 minutes. Measurement of Molecular Weight The values of [η] of degraded CPP were calculated according to Ref. [13]. The Mark-Houwink equation [14] [η] = 0.0174M 0.6919 was applied to determine the viscosity-average molecular weight of degraded CPP. Results and Discussion Determination of Kinetic Expression by Data Fitting Technique The common kinetic equations for ultrasonic degradation of polymers are as follows: Baramboim’s equation [15-18] 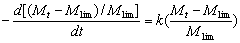 (1) (1)
where M0 and Mt express the molecular weight at time 0 and t respectively. Mlim is the limiting molecular weight and k expresses the rate constant of ultrasonic degradation. By integration, Eq. (1) can be expressed as: 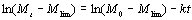 (2) (2)
(2) Ovenall’s equation [5] 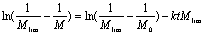 (3) (3)
Since 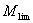 and and 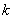 are all constants, according to Ref.[19], they can be merged into one constant. are all constants, according to Ref.[19], they can be merged into one constant. 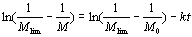 (4) (4)
(3) Giridhar Madras [7] suggested the following kinetic equation based on theoretic derivation: 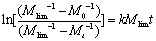 (5) (5)
It can be proved that Eq. (5) is consistent with Eq. (3) by a checking calculation. Therefore, Eq. (3) was used in this study. (4) Malhotra’s equation [3, 9, 16, 20] 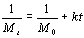 (6) (6)
To determine the expression of kinetic equations we need first to determine the parameters other than M0, M and t. The parameter k in Eq.(6) is easy to determine; when 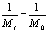 and t are plotted, k in Eq. (3) can be obtained from the slope of the regression equation. But Mlim and k in Eq. (2) and Eq.(3) are not easy to determine. In principle, obtaining Mlim, experiments must be conducted for a very long time until there is no further change in molecular weight. However, it is not easy or practical to conduct for a very long time. Consequently, the following experiential methods appear based on the experience of different researchers: (1) Xiuyuan et al. regarded the final experimental molecular weight as limiting molecular weight [15]. (2) Chakraborty et al. found that Mlim was approximately 80% of the molecular weight after 120 min of degradation when they measured Mlim at 3 h [2]. Then Chattopadhyay et al. obtained directly Mlim of poly (vinyl acetate) and poly (vinyl chloride) using this ratio [7]. Upon substitution of the dynamic equation in that article for Mlim, the fitting for experimental data was better. (3) When Li et al. investigated degradation dynamics of melt polymers for polyamide 6 [16], high-density polyethylene [17], polystyrene and EPDM [18], they selected Eq.(2) as dynamic model of these polymers. Then, Mlim and k were obtained according to the dynamic model that should well fit with the experimental data after substitution of Mlim and k. and t are plotted, k in Eq. (3) can be obtained from the slope of the regression equation. But Mlim and k in Eq. (2) and Eq.(3) are not easy to determine. In principle, obtaining Mlim, experiments must be conducted for a very long time until there is no further change in molecular weight. However, it is not easy or practical to conduct for a very long time. Consequently, the following experiential methods appear based on the experience of different researchers: (1) Xiuyuan et al. regarded the final experimental molecular weight as limiting molecular weight [15]. (2) Chakraborty et al. found that Mlim was approximately 80% of the molecular weight after 120 min of degradation when they measured Mlim at 3 h [2]. Then Chattopadhyay et al. obtained directly Mlim of poly (vinyl acetate) and poly (vinyl chloride) using this ratio [7]. Upon substitution of the dynamic equation in that article for Mlim, the fitting for experimental data was better. (3) When Li et al. investigated degradation dynamics of melt polymers for polyamide 6 [16], high-density polyethylene [17], polystyrene and EPDM [18], they selected Eq.(2) as dynamic model of these polymers. Then, Mlim and k were obtained according to the dynamic model that should well fit with the experimental data after substitution of Mlim and k. Now that Mlim is a parameter of the dynamic equation in order that it fits with the best experimental data, Mlim should be regarded as a parameter to be obtained along with k by the data fitting technique. If the dynamic equation is accurate, it should satisfy two conditions: firstly, fitting accuracy of the dynamic equation for experimental data is high; secondly, Mlim obtained by the data fitting technique should accord with or be close to the experimental limiting molecular weight obtained after a long time. If the data fitting technique is feasible, experiments need not be performed for a long time to acquire Mlim. This can save a great deal of investigation time. We adopt and develop Li’s method to determine Mlim and k to determine the dynamic equation of CPP in toluene solution. The difference is that we find the most suitable dynamic equation for CPP by comparing the fitting accuracy of many dynamic equations rather than using a single dynamic equation, and the particular process to determine the dynamic equation is expounded in this paper. Determination of Mlim and k in Kinetic Equations In data processing of experiments, when reviewing the accuracy of the regression equation Y = f (x) for fitting experimental datum x, the statistic remainder standard deviation (SE) is usually used as the evaluation index [21]. The calculation formula of SE is: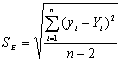 , where , where 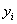 and Yi are the experimental value and calculated value of y at i point, respectively, and n is the number of experimental point. This method can also be applied to reviewing the accuracy of the kinetic equation of ultrasonic degradation for fitting molecular weights of polymers. The corresponding expression of SE for ultrasonic degradation is and Yi are the experimental value and calculated value of y at i point, respectively, and n is the number of experimental point. This method can also be applied to reviewing the accuracy of the kinetic equation of ultrasonic degradation for fitting molecular weights of polymers. The corresponding expression of SE for ultrasonic degradation is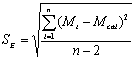 , where Mcal is the theoretical value of Mt calculated according to the kinetic equation. From the expression of SE, if SE becomes zero, Mcal will equal Mt and the kinetic equation will be completely precise. Certainly, the lower the value of SE, the higher is the accuracy of the kinetic equation. , where Mcal is the theoretical value of Mt calculated according to the kinetic equation. From the expression of SE, if SE becomes zero, Mcal will equal Mt and the kinetic equation will be completely precise. Certainly, the lower the value of SE, the higher is the accuracy of the kinetic equation. The steps to acquire Mlim and 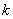 are as follows: are as follows: (1) Estimating a value of Mlim that is less than that of the final experimental molecular weight, the corresponding rate coefficient will be obtained at every datum point using Eq. (2) or Eq.(3). Here the rate coefficient is marked as Ki. (2) Calculating the average value of every ki, marked as k, which is the value of k in Eq. (2) or Eq.(3). (3) Putting Mlim and k back into Eq. (2) or Eq.(3) to calculate the molecular weight at every datum point, the calculated result is Mcal. (4) Modifying the value of Mlim and iterating (1)-(3) until a minimal SE is achieved. The corresponding Mlim and k are just the optimal values of Mlim and k in Eq. (2) or Eq.(3). (5) The values of SE using different kinetic equations are calculated to compare the fitting accuracy for experimental data. It is necessary to note that since the molecular weight of CPP before degradation is more than 170000 g/mol, the value of SE is very much higher than 1. Experimental Result of CPP Ultrasonic degradation of CPP was studied at different concentrations. The temperature was kept at 200C during the sonication and the ultrasound intensity was set at 440 W. It was found that the viscosity-average molecular weight of CPP decreased with time at each concentration. The decrease of molecular weight was greater at low concentrations than that at high concentrations. The experimental data listed in Table 1 show these results clearly. The Results of Data Processing for CPP by Common Kinetic Equations First, Eq.(2) is used to process the experimental data listed in Table 1. It is found that except for the set of data for 20%, the fitting accuracy is low. Namely, an error between the theoretical and experimental values is inherent in Eq.(2). The result is shown in Figure 1. The values of SE using Eq.(2) are listed in Table 2. 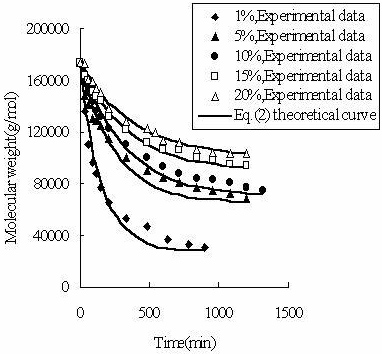
Figure 1. The fit of Eq. (2) to the measured molecular weight of CPP. Table 1. The viscosity-average molecular weight of CPP at different concentrations (g/mol). | | | 0 | 174000 | 174000 | 174000 | 174000 | 174000 | | 30 | 136000 | 148000 | 158000 | 164000 | 173000 | | 60 | 111000 | 141000 | 150000 | 160000 | 161000 | | 90 | 97000 | 130000 | 143000 | 152000 | 159000 | | 120 | 88000 | 129000 | 137000 | 147000 | 153000 | | 150 | 81000 | 125000 | 132000 | 144000 | 151000 | | 210 | 66000 | 114000 | 123000 | 133000 | 139000 | | 330 | 53000 | 100000 | 111000 | 122000 | 128000 | | 480 | 47000 | 91000 | 100000 | 112000 | 123000 | | 540 | - | - | - | - | 120000 | | 600 | - | 86000 | 94000 | 107000 | 113000 | | 630 | 37000 | - | - | - | - | | 720 | - | 81000 | 88000 | 106000 | 111000 | | 780 | 33200 | - | - | - | - | | 840 | - | 77000 | 84000 | 101000 | 107000 | | 900 | 30300 | - | - | - | - | | 960 | - | 75000 | 83000 | 98000 | 105000 | | 1080 | - | 72000 | 81000 | 96000 | 104000 | | 1200 | - | 69000 | 77000 | 94000 | 103000 | | 1320 | - | - | 75000 | - | - | | 3120 | 18000 | - | - | - | - | Table 2. The results of data processing for CPP by different kinetic equations. | | | 1% | 17000 | 6.79×10-8 | 10246 | 2944 | 7360 | 1866 | | 5% | 56000 | 4.91×10-8 | 8119 | 5869 | 16806 | 4096 | | 10% | 57500 | 3.42×10-8 | 6262 | 2695 | 13816 | 1925 | | 15% | 73000 | 3.14×10-8 | 3130 | 1565 | 12948 | 1449 | | 20% | 75000 | 2.25×10-8 | 2426 | 2634 | 8489 | 2824 | Then, Eq(3) and Eq.(6) are applied to process the experimental data of CPP. But the results are also unsatisfactory. The values of SE using Eq.(3) and Eq.(6) are also listed in Table 2. A New Kinetic Equation If 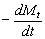 is defined as the rate of ultrasonic degradation, Eq.(2) can be written as: is defined as the rate of ultrasonic degradation, Eq.(2) can be written as: 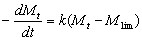 (7) (7)
Eq.(6) can be expressed as: 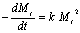 (8) (8)
If Eq. (7) is combined with Eq. (8) and the term of Mlim is added to Eq.(6), we suggest a new second order kinetic equation: 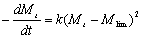 (9) (9)
By integration, Eq. (9) can be expressed as: 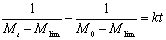 (10) (10)
According to the principle of the minimal SE, Eq.(10) is used to fit the experimental data listed in Table 1. As demonstrated in Figure 2, the equation describes well the experimental data listed in Table 2. 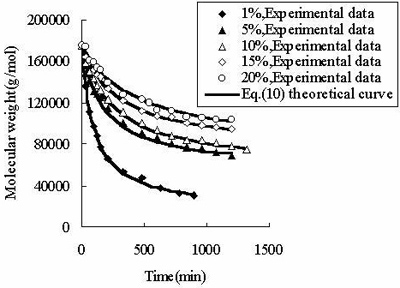
Figure 2. The fit of Eq. (10) to the measured molecular weight of CPP. In Table 2, for CPP concentrations of 1%~15%, the results of SE calculated using Eq.(10) are the lowest at all SE. The fitting accuracy of Eq.(10) is higher than for the other equations. Although the value of SE at 20% concentration is not the lowest, it is close to the lowest value, and the correlation coefficient of Eq.(10) at 20% concentration is 0.99, which is high enough to prove its accuracy. In order to verify whether the theoretical value of Mlim forecasted by Eq.(10) is correct, ultrasonic degradation was carried out for a long time at 1% concentration. As expected, the experimental Mlim was 18000 g/mol (Table 1), and the theoretical Mlim was 17000 g/mol (Table 2). Based on this, if the ultrasonic time is also prolonged at 5%~20% concentrations, the theoretical values of Mlim are also surely obtained. Therefore, ultrasonic degradation of CPP in toluene solution obeys the new second order kinetic equation-Eq.(10). The results described above prove that Mlim and k can be acquired by the data fitting technique. Analysis of the General Applicability of Eq.(10) In order to investigate the general meaning of Eq. (10), it is used to fit original data collected from the literature. The results are listed in Table 3. It is found that the accuracy of Eq. (10) is higher than for the kinetic equations in the existing literature. The values of SE demonstrate that Eq. (10) describes better the kinetic behaviour of some polymers than the kinetic equations in the literature. Thus, Eq. (10) is a new supplement for the traditional kinetic equations of polymers under ultrasonic irradiation. Table 3. Comparison of 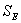 between Eq. (10) and kinetic equations in the literature. between Eq. (10) and kinetic equations in the literature. | | | 1 | Cyclohexyl(Solvent:toluene) | 12720 | 5968 | 85000 | | 2 | Isobutyl(Solvent: toluene) | 4961 | 4764 | 30000 | | 3 | Hexyl(Solvent: toluene) | 12283 | 9865 | 45000 | | 4 | Hexadecyl(Solvent: toluene) | 8753 | 3614 | 100000 | | 5 | N-butyl (Solvent: toluene) | 12031 | 2682 | 49000 | | 6 | Isopropyl (Solvent: toluene) | 26329 | 4345 | 65000 | | 7 | Isodecyl (Solvent: toluene) | 14016 | 719 | 65000 | | 8 | Lauryl (Solvent: toluene) | 16958 | 3745 | 130000 | | 9 | Octadecyl (Solvent: toluene) | 47657 | 6405 | 135000 | | 10 | Ethyl (Solvent: THF) | 6246 | 6237 | 5000 | | 11 | N-butyl (Solvent: THF) | 2963 | 2476 | 20000 | | 12 | Isobutyl (Solvent: THF) | 6665 | 5115 | 50000 | | 13 | Isodecyl (Solvent: THF) | 15706 | 7521 | 50000 | | 14 | Lauryl (Solvent: THF) | 12729 | 9630 | 60000 | | 15 | Isopropyl (Solvent: THF) | 30900 | 6654 | 60000 | | 16 | Hexadecyl (Solvent: THF) | 9058 | 1076 | 80000 | | 17 | Octadecyl (Solvent: THF) | 31566 | 7391 | 80000 | | 18 | Chitosan 0.2% 0°C | 20436 | 18956 | 17000 | | 19 | Chitosan 0.8% 0°C | 60916 | 57873 | 50000 | | 20 | Chitosan 1.4% 50°C | 78806 | 77459 | 84000 | | 21 | Polystyrene-L257 | 29146 | 15221 | 70000 | | 22 | Polystyrene-St8 45.5/364 | 23544 | 14123 | 31000 | The Relations Between k as Well as Mlim and the Concentration of CPP As demonstrated in Table 2, k decreases with increasing CPP concentration and Mlim increases with increasing concentration. This is in accord with the relation reported in the literature [5, 6, 9, 22]. Reduction of k implies that the rate of ultrasonic degradation slows down and increment of Mlim implies that the extent of ultrasonic degradation is lower. This indicates that the degree of ultrasonic degradation is more pronounced in the more dilute solution. This is attributed to the more intense entanglement between chains as the concentration increases. This entanglement represses the energy transfer between solvent and polymer [6, 10]. This causes the cavitation bubbles to become smaller and so the velocity gradients around the collapsing bubbles are lower at higher concentrations. Therefore, degradation efficiency decreases with increasing concentrations [9, 23]. Conclusions (1) Mlim of polymers under ultrasonic irradiation can be obtained by the data fitting technique. It is proved that the method is feasible and the result obtained by this method is reasonable. (2) Ultrasonic degradation of chlorinated polypropylene in toluene solution obeys the kinetic equation: 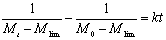
(3) Using the new kinetic equation proposed in this paper, the fitting accuracy for some experimental data collected from the literature is higher than that for kinetic equations in the literature. Our new equation can describe well the kinetic behavior of some polymers. This equation is a new supplement for traditional kinetic equations of polymers under ultrasonic irradiation. (4) The rate coefficient of ultrasonic degradation for CPP in toluene solution decreases with increasing concentration and Mlim increases with increasing concentration. The degree of ultrasonic degradation is more pronounced in the more dilute solutions. References 1. R.S. Mauler, F.M. Guaragna, D.L. Gobbi and D. Samios, “Sonochemical Degradation of 1,4-cis-polyisoprene Using Periodic Acid-solvent and Temperature Effect”, European Polymer Journal, 33 (2001) 399-402. 2. Jayanta Chakraborty, Jayashri Sarkar, Ravi Kumar and Giridhar Madras, “Ultrasonic Degradation of Polybutadiene and Isotactic Polypropylene”, Polymer Degradation and Stability, 85 (2004) 555-558. 3. Andre M.Striegel, “Influence of Chain Architecture on the Mechanochemical Degradation of Macromolecules”, J.Biochem.Biophys.Methods, 56 (2003) 117-139. 4. ZhongLei Fan, SiYe Tang, DaZhuang Liu and DongSheng Zhu, “Research Progress of Chlorinated Polypropylene”, China Modern Chemical Industry (Chinese), 12(2004) 16-19. 5. Hsing-YuanYen and Mu-Hoe Yang, “The Ultrasonic Degradation of Polyacrylamide Solution”, Polymer Testing, 22 (2003) 129-131. 6. Min Larng Tsaih, Lan Zang Tseng and Rong Huei Chen, “Effects of Removing Small Fragments with Ultrafiltration Treatment and Ultrasonic Conditions on the Degradation Kinetics of Chitosan”, Polymer Degradation and Stability, 86 (2004) 25-32. 7. Sujay Chattopadhyay and Giridhar Madras, “Influence of Temperature on the Ultrasonic Degradation of Poly(vinyl acetate) and Poly(vinyl chloride)”, Journal of Applied Polymer Science, 88 (2003) 2818-2822. 8. T. Miyazaki, C. Yomota and S.Okada, “Ultrasonic Depolymerization of Hyaluronic Acid”, Polymer Degradation and Stability, 74 (2001) 77-85. 9. Mohammad Taghi Taghizadeh and Abbas Mehrdad, “Calculation of the Rate Constant for the Ultrasonic Degradation of Aqueous Solutions of Polyvinyl Alcohol by Viscometry”, Ultrasonics Sonochemistry, 10 (2003) 309-313. 10. Farah Kanwal, John J.Liggat and Richard A. Pethrick, “Ultrasonic Degradation of Polystyrene Solutions”, Polymer Degradation and Stability, 68 (2000) 445-449. 11. A. Gronroos, P. Pirkonen and O. Ruppert, “Ultrasonic Depolymerization of Aqueous Carboxymethylcellulose”, Ultrasonics Sonochemistry, 11 (2004) 9-12. 12. ZhouXiaodong, Lin Qunfang, Dai Gance and Ji FaXiang, “Ultrasonic Degradation of polysilane Polymers”, Polymer Degradation and Stability, 60 (1998) 409-413. 13. ManJun He, WeiXiao Chen and XiXia Dong, “Molecular Weight of Polymers”, Polymer Physics (Chinese), ShangHai (1990) pp.174-180. 14. DaZhuang Liu, ZhongLei Fan, PeiQin Sun and XueRu Dong, “Solution Properties of Chlorinated Polypropylene and Maleic Anhydride Grafted Chlorinated Polypropylene”, Physics and Chemistry of Liquids, 42 (2004) 551-560. 15. Ni Xiuyuan, Hu Yuefang, Liu Bailin and Xu Xi, “Mechanical Degradation and Mechanochemical Copolymerization of Hydroxyethyl Cellulose”, European Polymer Journal, 37 (2001) 201-206. 16. Jiang Li, Mei Liang, Shaoyun Guo and Ying Lin, “Studies on Chain Scission and Extension of Polyamide 6 Melt in the Presence of Ultrasonic Irradiation”, Polymer Degradation and Stability, 86 (2004) 323-329. 17. Yuntao Li, Jiang Li, Shaoyun Guo and HuiLin Li, “Mechanochemical Degradation Kinetics of High-density Polyethylene Melt and Mechanism in the Presence of Ultrasonic Irradiation”, Ultrasonics Sonochemistry, 12 (2005) 183-189. 18. Jiang Li, Shaoyun Guo and Xiaonan Li, “Degradation Kinetics of Polystyrene and EPDM Melts Under Ultrasonic Irradiation”, Polymer Degradation and Stability, 89 (2005) 6-14. 19. He GuangBo, Chen KeQiang and Xu Xi, “Ultrasonic Degradation and Copolymerization of Poly(vinyl chloride) with Butyl Acrylate”, 11 (1995) 56-61. 20. J.P. Lorimer and T.J. Mason, “Some Recent Studies at Coventry University Sonochemistry Centre”, Ultrasonics Sonochemistry, 2 (1995) 81-86. 21. PeiQin Sun and DaZhuang Liu, “Linearity Regression”, Experiment Design, Data Processing and Computer simulation (Chinese), Zhenzhou, (2001)pp. 44. 22. Giridhar Madras and Sujay Chattopadhyay, “Effect of Benzoyl Peroxide on the Ultrasonic Degradation of Poly(vinyl acetate)”, Polymer Degradation and Stability, 73 (2001) 33-38. 23. A. Gronroos. P. Pirkonen, J. Heikkinen, J. Ihalainen, H. Mursunen and H. Sekki, “Ultrasonic Depolymerization of Aqueous Polyvinyl Alcohol”, Ultrasonics Sonochemistry, 8 (2001) 259-264. Contact Details Si-Ye Tang and Da-Zhuang Liu College of Chemical Engineering
Zhengzhou University
Zhengzhou 450002, China E-mail: [email protected] |