Introduction Photoconducting polymers doped with nonlinear optical chromophores have emerged as efficient and inexpensive photorefractive (PR) materials [1-5]. Since the first report of the organic polymer-based photorefractive materials in 1991 [6], PR polymers have been investigated intensively for their potential applications in dynamic volume holography, image formation, optical processing, reversible data storage, correlation, etc. [1-5, 7-10]. Recently, PR polymer composites gained a great amount of attention for its advantage of large PR effect, structural flexibility, and good processability. A typical photoconducting polymer consists of poly(9-vinylcarbazole) (PVK) doped with a small amount of sensitizer such as C60. Optical excitation of the sensitizer produces mobile holes/electrons, which drift under an applied electric field and are subsequently trapped. The resulting space charge electric field alters the refractive index of the chromophores through the electro-optic effect. The optimization of the effective electro-optic coefficient reff generally involves the synthesis of push-pull molecules with a strong permanent dipole moment and a large change in dipole moment upon excitation, as characterized by the molecular second order polarizability [11, 12]. Reorientation of the chromophores under the combined effects of the space charge and applied external electric fields leads to a modulated birefringence, further enhancing the refractive index modulation [13]. At room temperature, the orientation mobility can be enhanced with a plasticizer such as ethylcarbazole (ECZ). Chromophores such as 2-(p-chlorophenyl)-(3’-nitrobenzo[d])-(4’’-methoxybenzo[h])-1,3-dioxa-6-aza-2-boracyclonon-6-ene [14] (CB) are characterized by their permanent dipole moment μ and first hyperpolarizability β induced by asymmetric charge distribution (donor-acceptor molecules) conjugated through a pathway of π-electrons. We report here, PR polymers based on the CB chromophore. This compound derives from the well-known stilbene backbone, to which arylboron (ArB-) fragment has been added. This family of readily available macrocyclic boron compounds has recently attracted some interest from various perspectives in analytical and supramolecular chemistry [14, 15]. The CB molecules investigated so far have shown NLO properties in solution [14], however, in the solid state, these properties are canceled because they crystallize in centrosymmetric space groups. In order to break the symmetry in the crystal, we decided to explore the application of these chromophores in films. To evaluate the holographic performance of these kind of boronate derivatives in the PVK:ECZ matrix sensitized with C60, we measured the diffraction efficiency and the two beam coupling gain in a tilted four and two wave mixing geometry, respectively. We also evaluated the PR performance of these composites by changing the PVK:ECZ ratio. Acceptable photorefractive properties were observed for thick polymer films with a glass transition temperature Tg of 77°C. Experimental Synthesis Synthesis, chemical characterization and quadratic nonlinear optical properties (by EFISH technique) of CB (Figure 1a) are described in Ref. 14. We prepared samples with the following compositions: CB:PVK:ECZ:C60 i) 30:45:23.5:1.5 wt.%, ii) 35:42:21.5:1.5 wt.%, and iii) 30:55:13.5:1.5 wt.%. Chemical purity of the PR constituents is very important. CB was purified six times by recrystallization from dichloromethane. PVK was purchased from Aldrich (average MW ca. 1 100 000, Tg 200°C) and purified six times by column chromatography, dissolved in THF. ECZ (Aldrich) was purified three times by recrystallization from chloroform. C60 (Aldrich: 99.95%) was used as was received. Figure 1b) shows the linear optical absorption of CB:PVK:ECZ:C60. ![a) Chemical structure of CB: 2-(p-chlorophenyl)-(3’-nitrobenzo[d])-(4’’-methoxybenzo[h])-1,3-dioxa-6-aza-2-boracyclonon-6-ene, and b) linear optical absorption of sample CB:PVK:ECZ:C60 30:45:23.5:1.5 wt.%, sample thickness d = 110 mm.](/work/E6ZBM6R236UCIqxi2r01_files/image001.gif)
Figure 1. a) Chemical structure of CB: 2-(p-chlorophenyl)-(3’-nitrobenzo[d])-(4’’-methoxybenzo[h])-1,3-dioxa-6-aza-2-boracyclonon-6-ene, and b) linear optical absorption of sample CB:PVK:ECZ:C60 30:45:23.5:1.5 wt.%, sample thickness d = 110 μm. Sample preparation Magnetic stirring in dichloromethane dissolved the CB:PVK:ECZ constituents. C60 was previously dissolved in toluene and then mixed with CB:PVK:ECZ. The solution was filtered through a 20 μm pore size paper filter. The solvent was evaporated under reduced pressure on a rotary evaporator. The mixture was dried for 12 h in an oven at 60°C. Next, the dried material was melted and mixed between two large glass slides to removed the trapped air bubbles from the film. This step was repeated several times until the mixture was optically clear and uniform. A small piece of this film was melted between two ITO-coated glass slides at a temperature of 140°C. Calibrated glass spacers of 110μm were used to ensure a uniform sample thickness. Finally, samples were sealed with quick-setting epoxy adhesive. The ITO electrodes were previously cleaned by ultrasonic treatment in a distilled water and ethanol bath sequentially by 30 minutes. Four wave mixing (FWM) measurements The geometry used in the four waves coupling measurements is shown in Figure 2 a). The experiments were performed with a 10 mW He-Ne laser (λ = 632.8 nm). The two writing beams (“1” and “2”) had a power of ~ 1 mW each, were s-polarized, and were focused to spot sizes of ~ 1 mm at normal incidence on the sample. The angle between the beams outside the sample (2θo) was 21° and the tilt angle ψ was 60°. The formed grating with a period Λ is given by: 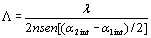 (1) (1)
where α1int and α2int are the beams angles inside the sample. The refractive index of the polymers composites, measured with a reflectometry system, resulted in n = 1.58 at 632.8 nm. From Eq. (1) it follows that grating spacing is Λ = 2.9 μm. The probe beam was p-polarized, had a power 2000 times smaller than the writing beams and was focused to a spot size of ~ 0.5 mm. The value of the external applied voltage was varied from 0 to 8 kV (E from 0 to 72.7 V/μm for a sample thickness d = 110 μm). The normalized diffraction efficiency is defined as the ratio of the intensity I of the diffracted beam and the intensity of the probe beam that is transmitted when no grating is being written in the sample by the writings beams. In a typical four wave mixing experiment, the intensity of the diffracted and transmitted beams is recorded as a function of the applied electric field. The normalized transmitted diffraction efficiency is then calculated as: 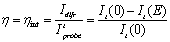 (2) (2)
The index modulation amplitude Δn is related to the normalized diffraction efficiency η by Kogelnik´s coupled-wave theory in a thick medium [16-18] that in a simplified version is: 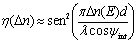 (3) (3)
where ψint is the tilt angle inside the sample. In Figure 2b) we can see the experimental setup for these diffraction experiments. 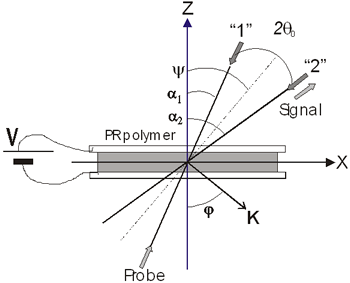
a) 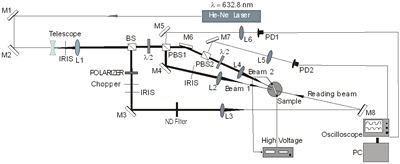
b) Figure 2. a) Geometry used in the four and two beam coupling measurements. In the latter case the probe beam is blocked. b) Experimental setup: M = mirror, L = lens, PBS = polarizing beam splitter, BS = beam splitter, λ/2 = half wave plate, ND = neutral density filter, PD = photodetector. For FWM, a Lab View interface was used to collect data. For TBC, additional two photodetectors were used. Two beam coupling (TBC) measurements Proof of the PR nature of the four wave mixing gratings is usually provided by the observation of asymmetric two beam coupling gain. These experiments were performed under the same angle parameters than FWM and with the same experimental setup of Figure 2 by just blocking the reading beam. In this case, writing beams were p-polarized in a 3.5:1 ratio. A general expression for the optical gain coefficient Γ can be obtained from Kukhtarev´s theory of dynamic self-diffraction in a photorefractive medium [1, 16, 19]. 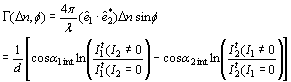 (4) (4)
where êi are the polarization vectors of the incoming beams, φ is the phase shift between the intensity pattern and the index modulation pattern. It1 and It2 are the transmitted intensities of writing beams “1” and “2”, respectively. Taking into account the absorption losses, the net optical gain (Γn) is defined as: Γn = Γ - α (5) where α is the absorption coefficient. For polymers with Tg below the measurement temperature, a possible figure of merit (FOM) for estimating the efficiency of the chromophores has been defined as [12, 20-22]: 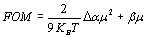 (6) (6)
where Δα is the polarizability anisotropy [8, 11-12, 23]. Results and Discussion The normalized diffraction efficiency as a function of the external applied electric field for samples with composition CB:PVK:ECZ:C60 are shown in Figure 3 for the following molecular concentrations: i) 30:45:23.5:1.5 wt.%, ii) 35:42:21.5:1.5 wt.%, and iii) 30:55:13.5:1.5 wt.%. 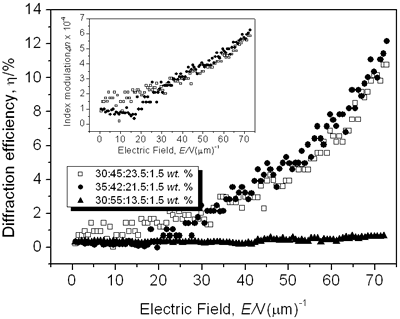
Figure 3. Normalized diffraction efficiency η as a function of the external applied electric field E using a p-polarized probe beam for CB:PVK:ECZ:C60 with the following molecular concentrations: 30:45:23.5:1.5 wt.% (open squares), 35:42:21.5:1.5 wt.% (filled circles), and 30:55:13.5:1.5 wt.% (filled triangles). Inset: Index modulation amplitude for samples with molecular concentrations of 30:45:23.5:1.5 wt.% (open squares) and 35:42:21.5:1.5 wt.% (filled circles). A LabView interface was used to collect data points. To assure steady state condition 100 data points we collected during 15 minutes. For p-polarized probe beam, compound i) showed a maximum diffraction efficiency > 10% while for ii) was > 12%. The larger the diffraction efficiency showed by the latter sample is explained simply by the higher concentration of the CB chromophore. In comparison with some highly efficient PR polymers that have been reported [7, 16, 24], the PR performance of our samples is rather small. However, these values are similar or even larger than those reported for other PR devices with higher chromophore content at the same applied external electric field E = 72.7 V/μm [25, 26] (diffraction efficiency increases with the fourth power of the external field [27]). Furthermore, in terms of photonic applications, with just 3% of diffraction efficiency is possible to have holographic reconstruction [27]. On the other hand, sample iii) showed a very small diffraction efficiency, note that for this sample the chromophore concentration was the same than i): 30 wt.%. It is clear here the importance of the ratio PVK:ECZ because, even when in iii) can exist larger hole mobility (higher amount of PVK), the orientation mobility of the chromophore´s dipoles is drastically reduced due to the smaller amount of plasticizer ECZ [28, 29]. These results are correlated with the Tg [23, 29-31] values we measured for our samples by using Differential Scanning Calorimetry (DSC). For instance, sample iii), exhibited a Tg of 85° while samples i) and ii) exhibited a smaller Tg: 77° and 74°, respectively. Nevertheless, for i) and ii), even at these relatively high Tg values, the formation time of the holographic grating was less than one second. We could not increase more than 35 wt.% the chromophore concentration because the incompatibility of the polar dye CB and the non-polar, plasticized polymer matrix. High CB concentration leads to phase separation, through a nucleation and growth mechanisms, as the polar dyes slowly crystallizes that render the composite opaque [8, 16, 25, 29, 32]. In regards to the refractive index modulation Δn of our samples, the inset of Figure 3 shows the values obtained from the FWM experiments and calculated from Eq. (3). The maximum Δn value was 5.8 × 10-4 for i) and 6.2 × 10-4 for ii) at E = 72.7 V/μm. Except for highly efficient PR polymers, these values are comparable to some previous PR reported with higher chromophore concentration [13]. CB has a permanent dipole moment of ~ 10 D [14], which is comparable to other chromophores [7, 16, 33]. The gain coefficient Γ for i) and ii) composites is shown in Figure 4. It was obtained from Eq. (4). Apparently, the optical gain for sample i) is bigger: 7.1 cm-1 at E = 72.7 V/μm than for sample ii) with a larger chromophore concentration: 6.1 cm-1 at E = 72.7 V/μm. However, at 633 nm, from Figure 1b), the absorption coefficient for sample i) is 73 cm-1. It means, from Eq. (5), that for these samples, and under our experimental conditions, we did not observe a net optical gain. 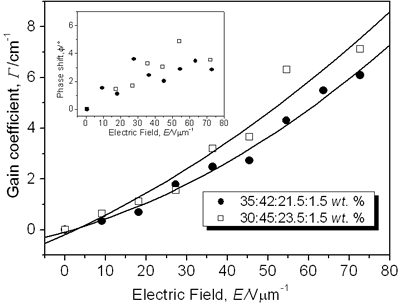
Figure 4. Optical gain coefficient Γ as a function of the external applied field E using a p-polarized writing beams for the composite CB:PVK:ECZ:C60 with the molecular concentrations of 30:45:23.5:1.5 wt.% (open squares) and 35:42:21.5:1.5 wt.% (filled circles). Solid lines are guides for the eye. Inset: A rough estimation values of the phase shift for samples with molecular concentrations of 30:45:23.5:1.5 wt.% (open squares) and 35:42:21.5:1.5 wt.% (filled circles). The smallest gain observed for samples with higher concentration could be due to a reduction in the optical quality that they exhibit. Samples ii) started to show phase separation and crystallization. Further, the stronger interaction of the p-polarized writing beams, than in FWM experiments, with the polymer dipoles, is a noisy-error factor for these TBC measurements that difficult precise energy exchange measurements. From Eq. (4) and Eq. (3) is possible to have an estimation of the phase shift φ (ê1 • ê2*= 0.99 for “p” polarized writing beams under our experimental conditions). For instance, for sample i) (see Table 1) with Γ = 7.1 cm-1 and Δn = 5.8 × 10-4 at E = 72.7 V/μm, φ = 3.6°. The inset of Figure 4 shows the rough estimation values of the phase shift. It is roughly, a slowly increasing function of the applied field. While the nonzero value of this phase shift still is a signature of the photorefractive effect [34-37], its low value shows that this material is not optimized for asymmetric energy exchange, even though it has a relatively large index modulation. Theoretically, an identical grating, but with a phase shift of 90°, would have a coupling coefficient of Γ = 114 cm-1. The phase shift φ of the index grating and the interference pattern is a function of many parameters, such as the trap density of the photorefractive centers, and the external applied electric field. If the only mechanism for charge transport is diffusion, the phase shift is equal to 90° according to the standard model for the photorefractive effect in inorganic crystals. For photorefractive polymers, however, a strong external electric field is necessary for charge photogeneration, high hole/electron mobility and orientational birefringence [1, 28, 38-42]. The drift of mobile charges under the applied electric field is the main mechanism for charge transport [28, 39] and will cause the phase shift to deviate from 90°. In most of the guest-host polymer composites, the values reported for the phase shift almost never approach 90° [16]. The values reported in the literature are often as small as 10-20° [16, 42]. Table 1 summarizes the results for the different samples we have characterized. Currently, we are investigating the NLO response of diorganotin derivatives [43] with an estimated β value of 1.5 times larger than that of the boron derivatives. Table 1. PR composites and their measured values for the holographic and Tg parameters. E = 72.7 V/μm, sample thickness d = 110 μm | | | i) 30:45:23.5:1.5 wt.% | 10.8 | 5.8 | 7.1 | 77 | | ii) 35:42:21.5:1.5 wt.% | 12.2 | 6.2 | 6.1 | 74 | | iii) 30:55:13.5:1.5 wt.% | 0.7 | 1.5 | - | 85 | Conclusions We fabricated PR composites functionalized with a boron derivative nonlinear chromophore. We have examined the diffraction efficiency, the optical gain coefficient, the phase shift, and the effect on the chromophore orientation at room temperature as a function of PVK:ECZ ratio of PR composites based on the dye 2-(p-chlorophenyl)-(3’-nitrobenzo[d])-(4’’-methoxybenzo[h])-1,3-dioxa-6-aza-2-boracyclonon-6-ene. From these PR properties and according to the amount of plasticizer and the Tg values measured by DSC (well above room temperature), the chromophore CB seems to have a very rigid structure that make difficult the dipole orientation at room temperature. In addition, the relatively low performance of our samples can be explained by the fact that, even when the permanent dipole moment of CB (~10 D) is comparable to other chromophores that form highly efficient PR devices, the introduction of an arylboron substituent leads to global reduction in the first hyperpolarizability β, arising from bent molecular geometry. The TBC coefficient at 633 nm was limited by the small phase shift between the intensity pattern and the holographic grating. In view of these results it would be interesting to explore some molecular modifications of these NL chromophores. We have initiated the investigation of the NLO response of diorganotin derivatives since these compounds present excellent planarity and they have been shown to give an increase in β of 1.5 with respect to the boron derivatives. Acknowledgements This work was supported by CONACyT (México) Grants G34629 and J40775-F, and CONCyTEG Grant 04-04-K117-011-07. We thank Dr. E. Arias-Marín from CIQA for the sample Tg (DSC) measurements. References 1. B. Kippelen, K. Meerholz and N. Peyghambarian in Nonlinear optics of organic molecules and polymers; H. S. Nalwa and S. Miyata eds., CRC Press, Inc.: Boca Raton, FL, (1997). 2. L. Solymar, D. J. Webb and A. Grunnet-Jepsen, in The physics and applications of photorefractive materials, Oxford University Press, Oxford, (1997). 3. Miyata and Sasabe Eds. “Lightwave manipulation using photorefractive polymers”, N. Peyghambarian, B. Kippelen, K. B. Ferrio, J. Herlocker, J. L. Maldonado, E. Hendrickx, S. Mery, A. Golemme and S. R. Marder, p. 223-232 in Light wave manipulation using organic nonlinear optical materials, (2000). 4. P. Günter, Ed., Nonlinear optical effects and materials, Springer-Verlag, Germany, (2000). 5. J. L. Maldonado and J. García M., “The photorefractive polymers, physics and photonic applications of these new materials”, Rev. Mex. Fís., 47 (2001) 582-601. 6. S. Ducharme, J. C. Scott, R. J. Tweig and W. E. Moerner, “Observation of the photorefractive effect in a polymer”, Phys. Rev. Lett., 66 (1991) 1846 -1849. 7. B. Kippelen, S. R. Marder, E. Hendrickx, J. L. Maldonado, G. Guillement, B. L. Volodin, D. D. Steele, Y. Enami, Sandalphon, Y.J. Yao, J.F. Wang, H. Rockel, L. Erskine and N. Peyghambarian, “Infrared photorefractive polymers and their applications for imaging”, Science, 279 (1998) 54-57. 8. D. J. McGee and M. D. Matlin, “Photorefractive polymers: materials science, thin film fabrication, and experiments in volume holography”, Am. J. Phys., 69 (2001) 1055-1063. 9. P. Dean, M. R. Dickinson and D. P. West, “Full-field coherence-gated holographic imaging through scattering media using a photorefractive polymer composite device”; Appl. Phys. Lett., 85 (2004) 363-365. 10. C. Hernández-Fuentes, J.Thomas, R. Termine, G. Meredith, N. Peyghambarian and B. Kippelen, “Video-rate compatible photorefractive polymers with stable dynamic properties under continuos operation”, Appl. Phys. Lett., 85 (2004) 1877-1879. 11. C. R. morylan, R. Wortmann, R. J. Twieg and I. H. McComb, “Improved characterization of chromophores for photorefractive applications”, J. Opt. Soc. Am., B, 15 (1998) 929-932. 12. B. Kippelen, F. Meyers, N. Peyghambarian and S. R. Marder, “Chromophore design for photorefractive applications”, J. Am. Chem. Soc., 119 (1997) 4559-4560. 13. M. D. Rhan, D. P. West and J. D. Shakos, “Photorefractive holographic contrast enhancement via increased birefringence in polymer composites containing electro-optic chromophores with different alkyl substituents”, J. Appl. Phys., 87 (2000) 627-631. 14. H. Reyes, B. M. Muños, N. Farfán, R. Santillan, S. Rojas-Lima, P. G. Lacroix and K. Nakatani, “Synthesis, crystal structures, and quadratic nonlinear optical properties in a series of push-pull boronates derivatives”, J. Mater. Chem., 12 (2002) 2898-2903. 15. T. D. James, K. R. A. Samankumara Sandanayake and S. Shinkai, “Saccharide sensing with molecular receptors based on boronic acid”, Angew. Chem., Int. Ed. Engl., 35 (1996), 1912-1922. 16. E. Hendrickx, J. F. Wang, J. L. Maldonado, B. L. Volodin, Sandalphon, E. A. Mash, B. Kippelen and N. Peyghambarian, “Synthesis and characterization of highly efficient photorefractive polymers composites with long phase stability”, Macromolecules, 31 (1998) 734-739. 17. H. Kogelnik, “Coupled wave theory for thick hologram gratings”, Bell Syst. Tech. J., 48 (1969) 2909-2947. 18. M. Stolka in Encyclopedia of polymer science and engineering, Vol. 11, H. F. Mark and J. I. Kroschwitz, Eds., John Wiley & Sons, New York, (1988), p. 154 19. B. L. Volodin, Sandalphon, K. Meerholz, B. Kippelen, N. V. Kukhtarev and N. Peyghambarian, “Highly efficient photorefractive polymers for dynamic holography”, Opt. Eng., 34 (1995) 2213-2223. 20. W. E. Moerner, S. M. Silence, F. Hache and G. C. Bjorklund, “Orientationally enhanced photorefractive effect in polymers”, J. Opt. Soc. Am., B, 11 (1994) 320-330. 21. R. Wortman, C. Poga, R. J. Twieg, C. Geletneky, C. R. Moylan, P.M. Lundsquist, R. G. DeVoe, P. M. Cotts, H. Horn, J. E. Rice and D. M. Burland, “Design of optimized photorefractive polymers: a novel class of chromophores”, J. Chem. Phys., 105 (1996) 10637-10647. 22. S. R. Marder, B. Kippelen, A.K. Jen and N. Peyghambarian, “Design and synthesis of chromophores and polymers for electro-optic and photorefractive applications”, Nature (London), 388 (1997) 845-851. 23. J. C. Ribierre, G. Cheval, F. Huber, L. Mager, A. Fort, R. Muller, S. Méry and J. F. Nicoud, “Direct comparison of mechanical and electro-optic responses of a low Tg photorefractive doped polymer”, J. Appl. Phys., 91 (2002) 1710-1712. 24. M. Eralp, J. Thomas, S. Tay, G. Li, G. Meredith, A. Schülzeng and N. Peyghambarian, “High-performance photorefractive polymer operating at 975 nm”, Appl. Phys. Lett., 85 (2004) 1095-1097. 25. E. J. Smiley, D. J. McGee, C. Salter and C. R. Carlen, “Diffraction efficiency and phase stability of poly(N-vinylcarbazole)-based photorefractive polymers composites as a function of azo-dye concentration”, J. Appl. Phy., 88 (2000) 4910-4912. 26. D. V. Steenwinkel, C. Engels, E. Gubbelmans, E. Hendrickx, C. Samyn and A. Persoons, “Fully functionalized photorefractive polymethacrylates with net gain at 780 nm”, Macromolecules, 33 (2000) 4074-4079. 27. S. Tay, J. Thomas, M. Eralp, S. Tay, G. Li, B. Kippelen, S.R. Marder, G. Meredith, A. Schülzeng and N. Peyghambarian, “Photorefractive polymer composite operating at the optical communication wavelength of 1550 nm”, Appl. Phys. Lett., 85 (2004) 4561-4563. 28. O. Ostroverkhova and K. D. Singer, “Space-charge dynamics in photorefractive polymers”, J. Appl. Phys., 92 (2002) 1727-1743. 29. R. Bittner, T. K. Daubler. D. Neher and K. Meerholz, “Influence of glass transition temperature and chromophore content on the steady state performance of poly(N-vinylcarbazole)-based photorefractive polymers”, Adv. Mater., 11 (1999) 123-127. 30. D. J. Binks, K. Khand and D. P. West, “Reorientation of chromophores in dispersive photorefractive polymers”, J. Opt. Soc. Am., B, 18 (2000) 308-312. 31. P. Acebal, S. Blaya and L. Carretero, “Hight Tg photorefractive polymers: influence of the chromophores´s β tensor”, J. Chem.. Phy., 121 (2004) 8602-8610. 32. E. Hendrickx, B. L. Volodin, D. D. Steele, J. L. Maldonado, J. F. Wang, B. Kippelen and N. Peyghambarian, “Phase stability of guest/host photorefractive polymers studied by light scattering experiments”, Appl. Phys. Lett., 71 (1997) 1159-1161. 33. E. Hendrickx, J. Herlocker, J. L. Maldonado, S. R. Marder, B. Kippelen, A. Persoons and N. Peyghambarian, “Thermally stable high-gain photorefractive polymer composites based on a tri-functional chromophore”, Appl. Phys. Lett., 72 (1998) 1679-1671. 34. W.-S. Kim, J.-W. Lee and J.-K. Park, “Enhancement of the recording stability of a photorefractive polymers composite by the introduction of a trapping layer”, Appl. Phys. Lett., 83 (2003) 3045-3047. 35. O.-P. Kwon, G. Montemezzani, P. Günter and S.-H. Lee, “High gain photorefractive reflection gratings in layered photoconductive polymers”, Appl. Phys. Lett., 84 (2004) 43-47. 36. E. Hendrickx, D. V. Steenwinkel, A. Persoons and A. Watanabe, “Photorefractive Polysilanes functionalized with a nonlinear optical chromophore”, Macromolecules, 32 (1999) 2232-2238. 37. T. Sassa, T. Muto and T. Wada, “Enhanced photorefractive two-beam coupling in low- Tg polymeric materials with a new device structure”, J. Opt. Soc. Am., B, 21 (2004) 1255-1261. 38. K. Khand, D. J. Binks and D. P. West, “Effect of field-dependent photogeneration on holographic contrast in photorefractive polymers”, J. Appl. Phys., 89 (2001) 2516-2519. 39. J. L. Maldonado, M. Bishop, C. Fuentes-Hernández, P. Caron, B. Domercq, S. Barlow, S. Thayumanavan, M. Malagoli, M. Manoharan, J.-L. Brédas, S. R. Marder and B. Kippelen, “Effect of substitution on the hole mobility of bis-diarylaminophenyl derivatives doped poly(styrene)”, Chem. Mater., 15 (2003) 994-999. 40. O. Ostroverkhova, A. Stickrath and K.D. Singer, “Electric field induced second harmonic generation studies of chromophore orientational dynamics in photorefractive polymers”, J. Appl. Phys., 91, (2002) 9481-9486. 41. A. Goonesekera and S. Ducharme, “Effect of dipolar molecules on carrier mobilities in photorefractive polymers”, J. Appl. Phys., 85, (1999) 6506-6514. 42. S. M. Silence, J. C. Scott, J. J. Stankus, W. E. Moerner, C.R. Moyland, G.C. Bjorklund and R. J. Twieg, “Photorefractive polymers based on dual-function dopants”, J. Phys. Chem., 99 (1995) 4096-4105. 43. H. Reyes, C. García, N. Farfán, R. Santillán, P.G. Lacroix, C. Lepetit and K. Nakatani, “Synthesis, crystal structures, and quadratic nonlinear optical properties in four push-pull diorganotin derivatives”, J. Organomet. Chem., 689 (2004) 2303-2310. Contact Details |