VIBRAPLANE Protects the Critical Subsystems of Large Equipment
There are natural frequencies in all equipment that have components. Generally, they exist in the 8 to 200 Hz environmental spectrum. Figure 46.1 demonstrates the transmissibility and resonant responses of three components in common equipment.
These components' Q or resonant responses surpass the allowable level set at Q=1.75 for this example. Figure 46.2 demonstrates the responses of the components above, following the introduction of isolation at 1 Hz. The roll-off isolator transmissibility reduces the input to the three critical components. With no alteration to the design of each component, their resonant responses are below the allowable limit, preventing any failure.

Image Credit: Kinetic Systems, Inc.
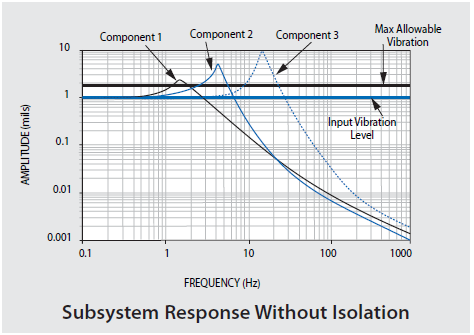
Figure 46.1. Internal Component Vibration Without Vibration-Free Table. Image Credit: Kinetic Systems, Inc.
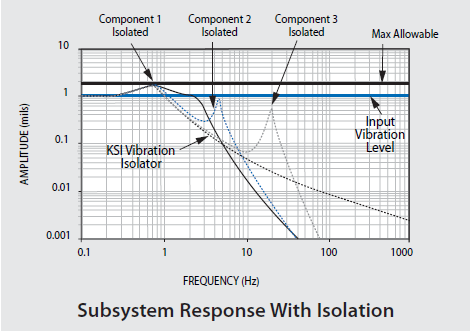
Figure 46.2. Internal Component Vibration Reduced With Vibration-Free Table. Image Credit: Kinetic Systems, Inc.
KSI Optical Tables...Better Built Through Better Design
KSI has removed all guesswork when choosing optical tables and vibration control equipment. Pre-engineered rigid and high natural frequency honeycomb optical tables, breadboards, and modular rigid supports with the option to upgrade to vibration isolators have been developed at KSI to provide cost-effective solutions for any vibration environment.
In severe or unknown vibration environments that require precise applications, highly damped honeycomb optical tables, like the 5300 Series and Active-Air vibration isolation systems, are recommended. The economical, broadband damped tables, like the 5200 Series or 5100 Series with isolators or the Modular Rigid Supports, are preferable for standard or moderate environments.
Understanding Optical Table Specifications
There is no standard practice for comparing optical tables from various manufacturers, and there is an abundance of unnecessary complexity regarding technical performance specifications offered by different manufacturers.
KSI emphasizes the important distinction between reality and specification hype. For example, flatness, stiffness, static deflection, weight, natural frequency, dynamic compliance, and damping are legitimate properties of any optical table and are directly measurable by standard techniques and instruments.
There are, however, manufacturers that make use of theoretical estimates of unverified, intangible performance parameters. When it comes to optical table comparison and selection, real measured data and test results cannot be overshadowed by theoretical computed estimates based on unproven hypotheses and idealized assumptions.
Consider the Basics When Selecting and Specifying Optical Tables
Technical jargon and overly complicated dynamic and static and deflection concepts are being utilized to sell optical tables and vibration isolation equipment. Becoming confused and distracted from what you need to know is very easy. Below are the key basics needed to feel confident when choosing an optical table or isolation system.
Control
Natural Frequency
Sinusoidal building vibrations typically occur between 6 and 60 Hz, so optical tables should have a high natural frequency (preferably above 90 Hz) to avoid coincidence with this prominent low frequency.
KSI provides one piece tables in common sizes up to 6 feet (1.83m) x 16 feet (4.88m) with low natural frequency of 90 Hz or better to prevent interaction with the resonance of building vibrations.
If the table’s length/width ratio is equal to or greater than 1.33, then the lowest frequency mode will be free-free bending, otherwise it will be free-free twisting. Large custom tables with special tooling can be manufactured, or one or more tables can be spliced together. These will have lower natural frequencies.
Static Deflection
Optical tables need to be rigid enough to limit relative deflection, or sag, between supports caused by their own weight. KSI’s proprietary damped rigid epoxy ensures this rigidity, and is not compromised by plastic or viscoelastic laminations.
The maximum static (1g) deflection of KSI tables in relation to their supports has been tested and adheres to simple beam deflection theory. Also of note is that the tables’ static deflections are far less than their flatness tolerances.
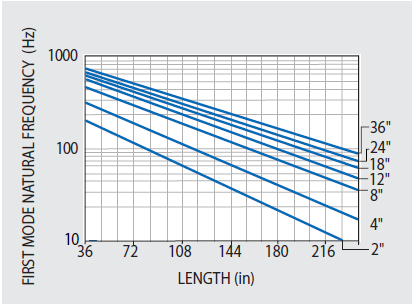
Figure 47.1. Undamped free-free bending mode frequency for KSI standard steel honeycomb optical tables with 3/16" thick top and bottom skins. Frequency is 10% less for tables with 1/8" skins. Apparent resonance of tables with tuned damping is 10% less. Image Credit: Kinetic Systems, Inc.
Deflection Due to Equipment Load
As well as minimizing static deflection, the high stiffness of KSI’s tables minimizes relative deflection caused by the weight of equipment and components installed on the table.
If installed equipment is consistently distributed across the table, then the additional table deflection caused by the equipment is decided simply by multiplying the deflection from Figure 47.2 by the (equipment/table) weight ratio.
If heavy equipment is being used, it is recommended that this deflection computation is repeated with various table lengths and thicknesses until an acceptably low value is obtained, perhaps 10%, of the precision needed for your application.
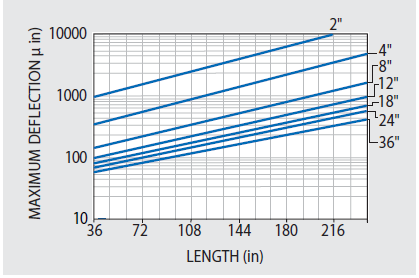
Figure 47.2. Maximum static (1g) deflection due to tables own weight of KSI optical tables relative to supports for 4' wide tables with 3/16" top and bottom skins. Deflection for 3' width is (1.3) and 5' width is (0.8) of plotted values. Multiply by 5.7 to convert from in/lbs to mm/N. Image Credit: Kinetic Systems, Inc.
Unit Load Deflection
The maximum relative deflection caused by a one-pound concentrated load on the center of the table should be minimal. In the example of the KSI table static weight deflection tests, results demonstrated that unit load deflections also align closely with simple beam deflection theory. To calculate the deflections caused by higher magnitude concentrated loads at the center, multiply the unit load values in Figure 47.3 by the higher load value. For instance, if looking for the deflection due to a 250 lb load, multiply the graph value by 250 for the chosen table size.
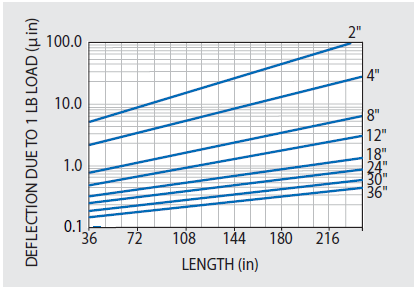
Figure 47.3. Unit load maximum deflections for KSI standard 4' wide optical tables with 3/16" thick top and bottom skins. Multiply by (1.3) for 3' table, and (0.8) for 5' table. Image Credit: Kinetic Systems, Inc.
Optical Table Weight
Figure 48.1 offers the approximate weights for 48" wide 5300 Series tables of varying standard thicknesses. The weights of other similar tables of various width and skin thickness can be estimated through multiplication of the values in Figure 48.1 by the ratios of their actual width/48" or their actual skin thickness/180" as appropriate.
The steel honeycomb optical tables are by nature structurally efficient and weigh far less than a solid steel or granite equivalent flat surface plate. However, a certain amount of weight is needed for stability and vibratory force resistance.
Thickness and length determine the table weight. Two rules to remember are:
- The table should weigh between 2.5 and 5 times that of the mounted equipment
- The minimum table thickness should be between 6% and 10% of the length.
These two rules can be used to decide on the minimum weight of your table selection. As an example, the minimum recommended standard thickness of a 10' long table in precision applications should be 8" or 12" thick.
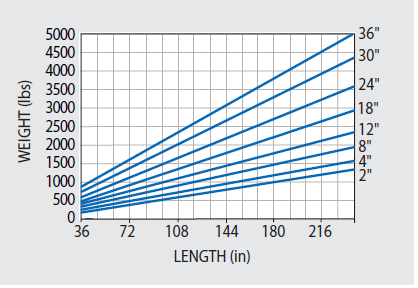
Figure 48.1. Approximate weights of 4' wide tables with 3/16" thick top and bottom skins. Weights of 3' and 5' wide tables are in direct proportion to width. Image Credit: Kinetic Systems, Inc.
Static and Dynamic Deflection and Compliance
It is standard practice in optical tables to quantify the dynamic deflection in terms of compliance, or more simply, the deflection response to a unit force. In static or steady-state conditions, compliance is identified as the “inverse” stiffness, or the flexibility in engineering units of deflection per unit force.

Image Credit: Kinetic Systems, Inc.
Figure 47.3 provides Unit Load Deflections and can be interpreted as a static compliance value graph at the center of the tables. By contrast, dynamic compliance is the deflection response caused by a unit vibratory force.
Vibration frequency, table resonance, and internal damping define the maximum response deflection. The dynamic response of the table at its corner, or corner compliance, is a standard measurement for comparing specifications.
Damping and Dynamic Compliance
Optical tables should have enough internal structural damping, or energy dissipation, to maintain control of their relative deflection resonant response to random high-frequency building vibration.
Internal damping limits modal resonant response to transient disturbances. The impressive damping properties in all Vibraplane Optical Tables are shown through the common compliance spectra which come in the technical data with each product.
The compliance spectra work in the same way as conventional transmissibility curves. They characterize the system response deflection, which includes resonant amplification, as a function of frequency. A low resonant response is an essential criteria when choosing optical tables.
The resonant Q factor, or maximum transmissibility of the lowest resonance mode for KSI Optical Tables, is set during production in the following range:
5300 Series Q = 2-6
5200 Series Q = 6-9
5100T Series Q = 9-13
5100H Series Q = 13-18
5100 Series Q = 18-25
The corresponding maximum compliance values for 5300 Series Tables are represented in Figure 48.2.
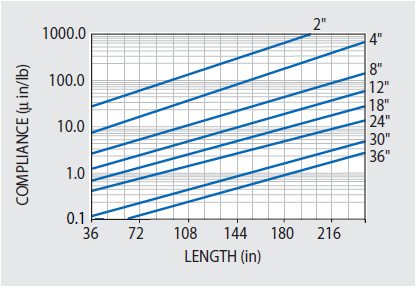
Figure 48.2. Maximum dynamic corner compliance at first resonance for our 5300 Series tables with 3/16" thick skins. Multiply these values by 4 for 5200 Series and 15 for 5100H Series and 5100 Series. Image Credit: Kinetic Systems, Inc.
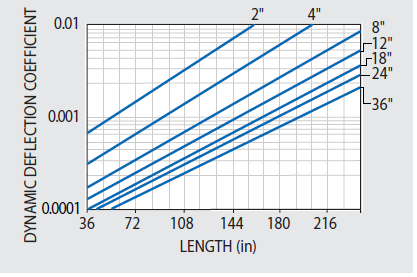
Figure 49.1. Dynamic deflection coefficient DDC for 4' wide 5300 Series. Consult KSI for 5200 Series, 5100H Series, and 5100 Series. Image Credit: Kinetic Systems, Inc.
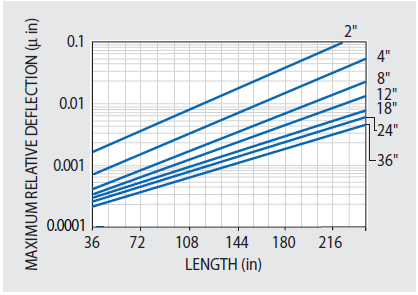
Figure 49.2. Maximum relative deflection (IRDmax) response for 4' wide vibration isolated 5300 Series in light traffic environment with Wa = 10-10 g2 Hz. Image Credit: Kinetic Systems, Inc.
To assist with the selection of optical tables, manufacturing specifications are provided, as well as real measured and verifiable dynamic and static table properties shown in Figure 49.2 and 47.1. For reference purposes, along with comparing to a variety of manufacturers’ calculated table specifications, it is important to know that no matter the model or price category, the calculated or predicted “Dynamic Deflection Coefficients” and “Maximum Relative Deflection” responses of KSI honeycomb tabletops are the industry’s lowest. This is demonstrated in Figures 49.1 and 49.2.
Theoretical Considerations in the Optical Table Relative Deflection Response Hypothesis
If it is assumed that the severity of laboratory floor vibration is statistical in nature and verifiably random, such as white noise, then the root mean square, or rms and relative deflection response, or RD, of an idealized stiff lumped mass single degree-of-freedom system will be defined as follows. 1
| RD = (y-x) = (WaQ g2 / 32π3fn3)1/2 = 12.25 (WaQ / fn3 )1/2 |
(8) |
Where:
| (Q / fn3)1/2 = (DDC) = Dynamic Deflection Coefficient of tabletop |
(9) |
Q = Resonant transmissibility of table
Wa = Floor Random Vibration Spectral Density,
(g2/Hz = floor mean squared vibration acceleration per 1 Hz band)
RDmax = (nonisolated) maximum
Relative Deflection of tabletop on rigid supports
Typical estimated random floor vibration conditions are:
Light traffic Wa = 10-10 g2/Hz
Heavy Traffic Wa = 10-9 g2/Hz
Light Manufacturing Wa = 10-8 g2
Hz Heavy Manufacturing Wa = 10-7 g2/Hz
The Dynamic Deflection Coefficient (DDC) for 5300 Series tables is derived from Equation Nine in union with natural frequency and Q data found in Figures 47.1 and 48.2 and plotted in Figure 49.1.
It is reasonable to assume in vibration analysis that an optical tabletop can be drawn as a rigid mass-spring-and-damper single-degree-of-freedom system up to its first resonance. The single-degree-of-freedom Equation 8 applies solely to a tabletop with no isolation supports.
If isolators are added, the system has further deflection coordinates or degrees-of-freedom and Equation 8 is not relevant. To address this in a simplified manner, the industry has offered two correction factors and an adapted interpretation of damping parameter Q. The correction factors are:
- Multiply Equation 8 by isolator transmissibility assumed as T =1% at high frequency to remove one degree-of-freedom,
- Multiply by two for a discretionary worst case,
- Use the apparent Q from the corner compliance tests utilized to arrive at Figure 49.2.
The latter Q is referred to as apparent because it contains rotation and translation response motions rather than one degree-of-freedom as theoretically required.
The resulting equation for Isolated Maximum Relative Deflection (IRD max) for a vibration isolated tabletop is the following:
| IRDmax = 12.25 (WaQ / fn3)1/2 x 0.02 |
(10) |
The Maximum Relative Deflection of vibration-isolated 5300 Series tabletops is derived from Equations 8 and 10 in relation to Figure 49.1 and is demonstrated in Figure 49.2 for easy reference.
References and Further Reading
- Crede, C.E. “Failure Resulting From Vibration”, Random Vibration, Volume 2, Edited by S.H. Crandall, MIT Press, 1963

This information has been sourced, reviewed and adapted from materials provided by Kinetic Systems, Inc.
For more information on this source, please visit Kinetic Systems, Inc.