Factors to Enhance Thermal Conductivity of ß-Si3N4 Ceramics (Review)

Koji Watari, Kiyoshi Hirao, Manuel E. Brito, Motohiro Toriyama and Kozo Ishizaki

Copyright AD-TECH; licensee AZoM.com Pty Ltd.

This is an AZo Open Access Rewards System (AZo-OARS) article distributed under the terms of the AZo–OARS https://www.azom.com/oars.asp which permits unrestricted use provided the original work is properly cited but is limited to non-commercial distribution and reproduction.

AZojomo (ISSN 1833-122X) Volume 2 January 2006

Topics Covered

Abstract

Keywords

Introduction

Intrinsic Thermal Conductivity

Thermal Conductivity Data of Si₃N₄ Ceramics

Effect of Density and β-phase Content

Effect of the Sintering Technique

Effects of the Sintering Aid

Effects of the Sintering Temperature

Quality of the Raw Powders

Effects of the Grain Orientation

Phenomenal Factors to Increase Thermal Conductivity

Thermal Conductivity Data of β-Si₃N₄ Grains

Thermal Conduction Mechanisms of β-Si₃N₄ Ceramics

Controlling Factors on the Conductivity

Crystal Defects into β-Si₃N₄ Grains

Thermal Conduction Mechanisms of β-Si₃N₄ Ceramics

Controlling Factors on the Conductivity

Crystal Defects into β-Si₃N₄ Grains

Phonon Mean Free Path

Grain Size

Thermal Anisotropy

Y₂O₃ Additive

Conclusions

Acknowledgements

References

Contact Details

Abstract

Researches on processing β-Si₃N₄ ceramics and their thermal conductivity are reviewed.  Empirical thermal conductivities of β-Si₃N₄ ceramics have been reported to be in the range of 10 to 162 Wm^-1K^-1 at room temperature, and are greatly affected by processing parameters such as purity of raw powders, type and amount of sintering aids, and forming as well as sintering conditions.  High thermal conductivities of greater values than 150 Wm^-1K^-1 have been achieved by fully densification, Y₂O₃ addition, and formation as well as alignment of large elongated β-grains.  Experimental observation and theoretical calculation clarify that the type and amount of crystal defects into β-Si₃N₄ grains as well as grain orientation are significant factors determining the thermal conductivity of sintered Si₃N₄ ceramics.

Keywords

Silicon nitride, Thermal conductivity, Crystal defects, Sintering, Sintering aid

Introduction

Si₃N₄ is inherently strong because of the covalent chemical bond between Si and N.  There are two isomorphic forms of Si₃N₄, i.e., α-Si₃N₄ and β-Si₃N₄ [1], which have a crystalline structure containing SiN₄ tetrahedra forming a corner-shared three-dimensional network with the characteristics (001) plane of a hexagonal structure.  The stacking of the planes is different in α and β structures, and is ABCD in α-Si₃N₄ and AB or CD in β-Si₃N₄ [1].

β-Si₃N₄ ceramics are currently used in engineering applications.  α-Si₃N₄ ceramics are unstable and convert to stable β-Si₃N₄ at high temperatures.  Furthermore, rod-like β-Si₃N₄ grains, bonded together and reinforcing each other are formed through a glassy phase as a secondary phase through sintering.  This makes β-Si₃N₄ difficult to fracture [2].  Hence, β-Si₃N₄ ceramics have been strongly favored compared to α-Si₃N₄.  Studies on processing, microstructure and mechanical properties of β-Si₃N₄ ceramics have been actively carried out for more than two decades.  In recent years, researches on enhancing fracture toughness and strength by applying the concept of self-reinforcement and introducing nm-sized β-Si₃N₄ have received increasing attention.  Very high strength (greater than 1.5 MPa) ceramics [3, 4], high fracture toughness (more than 10 MPam^0.5) ceramics [5] and high strength with high fracture toughness ceramics [6] have been developed through controlling size, shape and orientation of rod like β-Si₃N₄ grains.

Thermal conductivity is an important physical property of β-Si₃N₄ ceramics, and determines practically the reliability and performance of components in many industrial applications, because the thermal conductivity strongly influences the rate of heat dissipation.  As for automotive engines, low thermal conductivity is desired for heat insulation components to decrease fuel consumption, while high conductivity is required for cooling components with good thermal shock resistance.  In this review, we have summarized results of the thermal conductivity of β-Si₃N₄ ceramics obtained under various conditions.

Intrinsic Thermal Conductivity

Extensive investigation and evaluation of high-thermal-conductivity non-metallic solids were conducted between 1960 and 1985, and have been systematically summarized by Slack et al. [7]. Thermal conductivity measurements showed that natural and synthetic diamond, cubic BN, SiC, BeO, BP, AlN and Si were high-thermal-conductive solids with values of greater than 100 Wm^-1K^-1 at room temperature.  Among them, many researches on the conductivity diamond and AlN are actively carried out.  Impurities such as nitrogen atoms in diamond and oxygen atoms in AlN affect significantly their thermal conductivity.  The relationship between experimental thermal conductivity and impurities concentration of high purity nonmetallic solids indicates that intrinsic thermal conductivities at room-temperature of diamond and AlN are 2000 and 319 Wm^-1K^-1, respectively (see Table 1) [7, 8].  On the other hand, intrinsic values for SiC, BeO, BP and Si were estimated from the temperature dependence of the conductivity of these single crystals and ceramics, and were reported to be 490, 370, 360 and 156 Wm^-1K^-1, respectively [7].

The intrinsic thermal conductivity (κ_intrinsic) of nonmetallic solids in the temperature range T ≥ θ_D, where θ_D is the Debye temperature, can be described by the following equation [8]:

κ_intrinsic = BMδθ_D³ / (Tγ²)       (1)

where B is a constant, M the average mass of atoms in the crystal, δ³ the average volume occupied by one atom of the crystal, T the absolute temperature and γ the Gruneisen's constant [7-10].  Slack found a proportional relationship between the intrinsic conductivity of nonmetallic solids calculated from impurity concentration and the value of Mδθ_D³ at 300 K, and predicted that intrinsic values at room-temperature of BN and GaN are 760 and 130 Wm^-1K^-1 [7], respectively.  Table 1 also shows values of κ_intrinsic, θ_D, M, δ, γ, and Mδθ_D³of high-thermal-conductive solids.  The results suggested that materials with a higher Debye temperature, a lower atomic mass, and a simpler crystalline structure would have higher intrinsic thermal conductivities [7]. 

It is interesting to compare values of θ_D, M, δ and γ of both high-thermal-conductivity nonmetallic solids and Si₃N₄.  The values for β-Si₃N₄ are θ_D = 1100K [10], M = 20.0 g, δ = 0.218 nm [11] and γ = 0.72 [11], as shown in Table 1.  These values are almost equal to those of SiC : θ_D = 1080 K, M = 20.1 g, δ = 0.218 nm and γ = 0.76 [7], and AlN : θ_D = 950 K,  M = 20.5 g, δ = 0.218 nm and γ = 0.77 [8].  The result implies that β-Si₃N₄ satisfies the conditions for high thermal conductivity.

Watari et al. estimated the upper limit of the intrinsic conductivity of β-Si₃N₄ by using a proportional relation between the intrinsic conductivity and the value of Mδθ_D³ to be 400 Wm^-1K^-1 at room temperature [12].  Haggerty and Lightfoot stressed that SiC and β-Si₃N₄ are nearly identical, except for the number (n) of atoms in each primitive cell, and reported that the predicted intrinsic value is ~200 Wm^-1K^-1 for n = 14, and ~320 Wm^-1K^-1 for n = 7 [13].  The measurement of the thermal conductivity of β-Si₃N₄ grains indicates a value of 180 Wm^-1K^-1 at room temperature [14].

Thermal Conductivity Data of Si₃N₄ Ceramics

Effect of Density and β-phase Content

There are many reports on thermal conductivity of β-Si₃N₄ ceramics since 1976 [15-28].  Representative data of the room-temperature values are summarized in Table 2.  The temperature dependence of the conductivity of various β-Si₃N₄ ceramics [10, 16, 24, 28] is also shown in Figure 1.

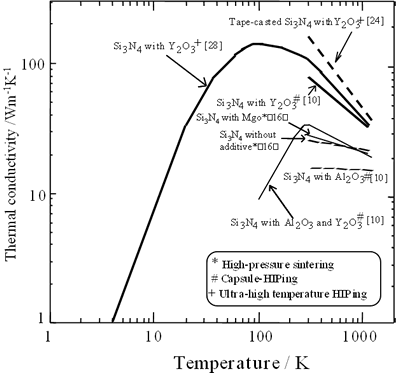
Figure 1. The temperature dependence of the conductivity of various β-Si₃N₄ ceramics

The values at room temperature are in the 10-162 Wm^-1K^-1 range.  The conductivity at room temperature and the temperature dependence of the conductivity are significantly influenced by bulk density, β-phase content and processing parameters. Figure 2 shows the relationship between the conductivity at room temperature and relative density of various β-Si₃N₄ ceramics.

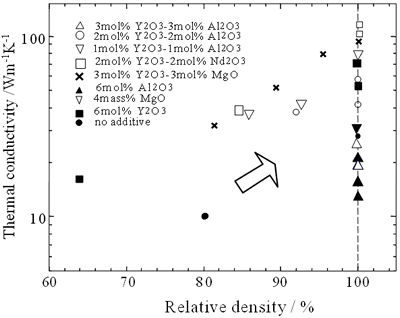
Figure 2. The relationship between the conductivity at room temperature and relative density of various β-Si₃N₄ ceramics

The data were obtained from references [16, 19, 22].  The conductivity increases as the relative density of the specimens increases, however is in the range of 15 to 120 Wm^-1K^-1 depending on type of sintering aids for fully densified samples.  The β-phase content also affects the conductivity of sintered materials as shown in Figure 3.

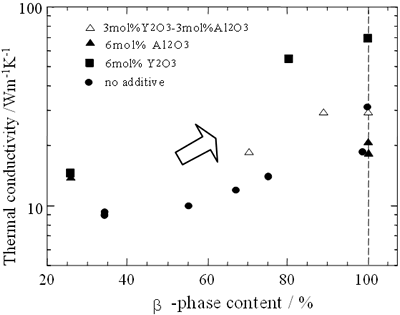
Figure 3. Thermal conductivity of Si₃N₄ ceramics as a function of β-Si₃N₄ content.  The amount of β-Si₃N₄, β-Si₃N₄/( α-Si₃N₄ +β-Si₃N₄), was calculated by comparing XRD peaks of α-Si₃N₄ (210), (201)

Though the conductivity increases as the β-phase content increases, the variation of the conductivity is strongly influenced by the type of sintering aid.  The changes of relative density and β-phase content of sintered materials are due to differences in processing parameters.  In the following section, effects of processing parameters on the conductivity of β-Si₃N₄ ceramics are summarized.

Table 1. Values of intrinsic thermal conductivity (κ_intrinsic), Debye temperature (θ_D), average mass (M), average volume occupied by one atom (δ ³), Gruneisen’s constant (γ) and M δθ_D³ of high-thermal-conductivity nonmetallic materials_.  Data were obtained from references [7-11].

Table 2: Representative data of thermal conductivity at room-temperature of β-Si₃N₄ ceramics.

The specimen obtained by reaction-bond sintering had relative density of 85%, while other specimens reached full densification. The β-phase content of all the specimens was 100%.

Effect of the Sintering Technique

Sintering techniques such as reaction-bond sintering [18], high-pressure sintering [16], capsuled-HIPing [10, 19], gas-pressure sintering [20-22], and ultra-high temperature HIPing [24] have been employed to obtain β-Si₃N₄ ceramics.  Reaction-bond sintering, in which metallic Si reacts with N₂ or NH₃ to form Si₃N₄, is a cost-effective method.  In this case, however, densified materials are difficult to obtain, and their relative density is usually less than 85% [18].  For this reason, conductivity of the reaction-bond sintered Si₃N₄ is only 17 Wm^-1K^-1, and is much less than those of specimens obtained by other methods [18].  High-pressure sintering, in which the specimen is fired under a high mechanical pressure by a cubic anvil apparatus, can produce fully densified β-Si₃N₄ with and without sintering aids.  Tsukuma et al. have successfully produced a dense β-Si₃N₄ by high-pressure sintering without sintering aids at 1900°C under 3 GPa.  The conductivity at room temperature was 30 Wm^-1K^-1, and is almost equal to that of a high-pressure sintered material with MgO addition [16].

Capsuled-HIP process is a method to produce densified ceramics by encapsuling a green body in a vitreous container, followed by firing under high gas pressures of greater than 50 MPa at relatively low firing temperatures compared with other sintering techniques.

The conductivity at room temperature of dense β-Si₃N₄ obtained by capsuled-HIPing at 1750°C for 1 h was 18 Wm^-1K^-1 for 6 mol% Al₂O₃ addition, and 72 Wm^-1K^-1 for 6 mol% Y₂O₃ addition [19].

For gas-pressure sintering, a high N₂ pressure allows higher firing temperature without thermal decomposition of Si₃N₄, and in addition, the higher formation of large rod like grains [29].  This benefit develops high thermal conductivity.  Gas-pressure sintered β-Si₃N₄ with a value of 80 Wm^-1K^-1 was successfully fabricated by firing at 1900°C by Li et al. [20].  Hirosaki et al. obtained a β-Si₃N₄ ceramic with a significant value of 120 Wm^-1K^-1 by gas-pressure sintering at 2000°C for 4 h with dopants of 0.5 mol% Y₂O₃ and 0.5 mol% Nd₂O₃ [21, 22].

Ultra-high temperature HIP process consists of firing at higher temperatures than 2000°C under gas pressures higher than 100 MPa.  Watari et al. produced a β-Si₃N₄ ceramic by HIPing at 2400°C for 2 h under a N₂ gas pressure of 200 MPa, and reported that the specimen had a conductivity of 107 Wm^-1K^-1 at room temperature [28, 30].  The conductivity at 4 to 1100 K of this material [28] is also presented in Figure 1.  A remarkable high conductivity at room temperature of 155 Wm^-1K^-1 was achieved by HIPing of tape-casted β-Si₃N₄ at 2500°C in a N₂ gas pressure of 200 MPa, along the tape-casting direction [24].

Effects of the Sintering Aid

Type and amount of sintering aids strongly influence the densification and the thermal conductivity of Si₃N₄.  It has been commonly accepted that the aids react with silica on the surface of Si₃N₄ particles to form a eutectic liquid during sintering, which promotes the densification.  Recently, however, it has been shown that the surface of Si₃N₄ does not consist of silica phase [31-35].  The reaction is probably more complex than simply SiO₂ involved one.  Since the presence of pores in sintered bodies considerably reduces thermal conductivity as shown in Figure 2, pore removal and densification are important.  Numerous studies have been performed to find an appropriate aid, and single addition of Al₂O₃, MgO, Y₂O₃ and rare-earth oxides, and concurrent additions of these additives have been reported to be useful to sinter Si₃N₄ [36].

The thermal conductivities of β- Si₃N₄ with various sintering aids such as Y₂O₃, Al₂O₃, MgO and Nd₂O₃ are shown in Table 2.  In the case of single addition of Y₂O₃, high thermal conductivities were always obtained.  The conductivity at room temperature was 72 Wm-1K-1 for capsuled-HIPing with 6 mol% Y₂O₃ addition [19], and 107 Wm-1K-1 for ultra-high temperature HIPing with 3.5 mass% Y₂O₃ addition [28, 30].  Very high conductivity, 155 Wm-1K-1 along the tape-casting direction, was obtained in textured β- Si₃N₄ with Y₂O₃ alone [24].  On the other hand, the conductivity of β- Si₃N₄ ceramics was 29 Wm-1K-1 for MgO addition [16] and 18 Wm-1K-1 for Al₂O₃ addition [19].

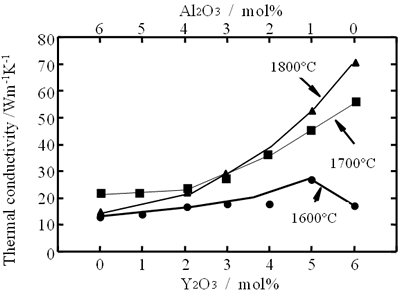
Several reports on the influence of concurrent additions have also been published.  Watari et al. seek the effects of aid ratio on the conductivity of capsuled-HIPed specimens with a constant quantity of Y₂O₃ and Al₂O₃ additives, and found that the conductivity decreased with increasing Al₂O₃ content [19], as shown in Figure 4.  The effects of total aid content were investigated by Hirosaki et al. [22].  Using their results, data are reorganized to show the effects of sintering aids and sintering temperature in Figure 5.  The conductivity is affected by the total amount of aids, and the highest conductivity was achieved when the total amount in the Y₂O₃-Nd₂O₃ and Y₂O₃-Al₂O₃ systems was 1 mol% [22].

Diverse patterns of temperature dependence of the conductivity are observed according to the type of additives (Figure 1).  A strong temperature dependence is found for single addition of Y₂O₃ [10, 24, 28].  Weak temperature dependence is observed for single addition of MgO [16] or Al₂O₃ [10], concurrent additions of Y₂O₃-Al₂O₃ [10] and without any addition [16].

Effects of the Sintering Temperature

Relationship between the conductivity and the sintering temperature is also shown in Figures 4 and 5.  As for single addition of Y₂O₃ (see Figure 4) and concurrent addition of Y₂O₃ and Nd₂O₃ (see Figure 5 (a)), a significant increase of the conductivity with increasing temperature is shown.  On the other hand, in the case of Y₂O₃-Al₂O₃ additives, firing temperature dependence of the conductivity is greatly influenced by the quantity of the additives.  The temperature dependency of the conductivity is strong, when small amounts of additives are used, and not significant when large amounts of additives are used.

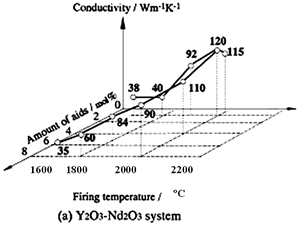
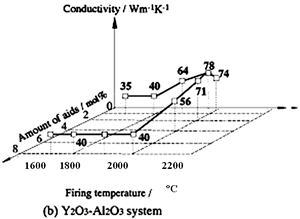
Figure 5. Effects of total aid content and firing temperature on thermal conductivity of β-Si₃N₄ ceramics.  The specimens were fired for 4 h at 1700°C and 1800°C in 1 MPa N₂ gas, at 1900°C in 10 MPa N₂ gas, and at 2000°C in 100 MPa N₂ gas.  Ratio of additives (Y₂O₃:Nd₂O₃ and Y₂O₃:Al₂O₃) is 1:1 in mole.

Quality of the Raw Powders

The type of raw powders also affects the conductivity.  Detectable impurities in the raw powders are oxygen, carbon, iron, calcium, aluminum, fluorine and chlorine [37, 38].  The oxygen concentration in the raw powders usually amounts to 0.5-3 mass %.  Watari et al. reported firstly that β-Si₃N₄ materials obtained from raw α-Si₃N₄ powders with lower oxygen content present higher conductivity [10].  Carbon impurity in the raw powders and in the sintered specimens should be also taken into account, since the concentration is usually from 100 to 10,000 ppm (in mass).  Studies concerning the effect of carbon impurity indicate that carbon content with a level of several thousand ppm results in a slight decrease of the conductivities of about 3 Wm^-1K^-1 [39].  Commercially available raw powders always contain metallic impurities, however the effects of metal and metal oxide impurities on the conductivity have not been investigated yet.

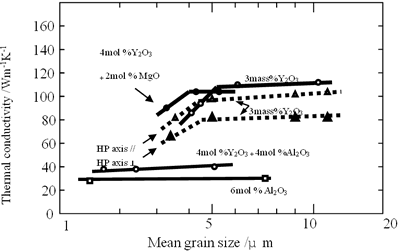
Figure 6. Relationship between thermal conductivity and mean grain size of β-Si₃N₄ ceramics.  All the samples were fully densified.  The change of grain size was carried out by annealing at various firing temperatures under high N₂ gas pressure of 200 MPa. Mean grain size was determined from photographs of polished and etched surface using the linear intercept method.

Effects of the Grain Orientation

Since β-Si₃N₄ grain has intrinsically fiber-like shape, anisotropic microstructure is developed in sintered β-Si₃N₄ through selected forming processes [6, 24, 27].  Figures 7 (a) and (b) show the microstructure of non-oriented [28] and oriented [24] β-Si₃N₄ ceramics, respectively.  The sample of Figure 7 (a) was obtained by HIPing at 2500°C, and the sample of Figure 7 (b) was produced through tape-casting with β-Si₃N₄ single crystal particles as seeds, and subsequently HIPing at 2500°C.  The microstructure of non-oriented specimens consists of large elongated grains with ~8 μm in diameter and ~60 μm long, and small grains with size of ~3 μm.  The conductivity of this material was 110 Wm^-1K^-1 at room temperature [28].  The tape-casted and HIPed specimen exhibits a highly anisotropic microstructure with extremely large elongated grains of ~10 μm in diameter and ~100 μm long highly oriented in the tape-casting direction, and small grains located in the interstices between very large grains.

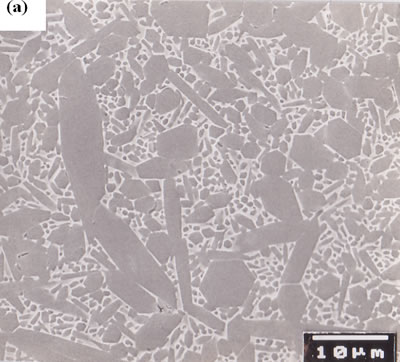
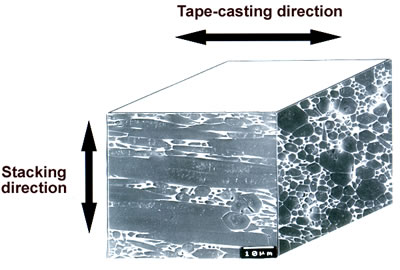
Figure 7. Microstructure of polished surfaces (a) ultra-high temperature HIPed specimen with 3.5 mass% Y₂O₃ additive, and  (b) tape-casted and ultra-high temperature HIPed specimen with  5 mass% Y₂O₃ additive and 5 vol% β-Si₃N₄ single crystal particles.  Both the specimens were fired at 2500°C for 2 h under a N₂ gas pressure of 200 MPa.  The polished surfaces of ultra-high temperature HIPed specimen were chemically etched, and those of tape-casted and ultra-high temperature HIPed specimen were plasma-etched.  The thermal conductivity at room temperature of the ultra-high temperature HIPed specimen was 110 Wm^-1K^-1, and the thermal conductivities of tape-casted and ultra-high temperature HIPed specimens were 155 and 52 Wm^-1K^-1 in the tape-casting and sheet-stacking directions, respectively.

The conductivities of the tape-casted and HIPed specimens were different depending on the casting direction, and were 155 and 52 Wm^-1K^-1 in the tape-casting and sheet-stacking directions, respectively [24].

Extruding with seed particles also produced a highly anisotropic microstructure and anisotropic conductivities.  Akimune et al. fabricated an extruded and sintered β-Si₃N₄ with conductivities of 162 and 85 Wm^-1K^-1 in the longitudinal and transverse extruding direction, respectively [27].  Effects of grain orientation on the conductivity should be thoroughly investigated.

Phenomenal Factors to Increase Thermal Conductivity

Specimens with high bulk density, β-phase content, large grains and strong anisotropic microstructure have high thermal conductivity as demonstrated above. Phenomenal factors enhancing the conductivity are summarized from the relationship between the processing parameters and thermal conductivity of β-Si₃N₄ ceramics, and are shown in Figure 8.  In the case of non-oriented Si₃N₄ materials, the thermal conductivity was as high as 80 Wm^-1K^-1 at room temperature under conditions of fully densification and phase transformation from α to β with Y₂O₃ addition [19, 20].  Further increase of the conductivity is achieved by remarkably grain growth, and its conductivity reaches to a value of 120 Wm^-1K^-1 [21, 22, 28, 30].  Formation and orientation of very large β-grains are considerably effective to increase the conductivity.  Highly oriented β-Si₃N₄ ceramics present high thermal conductivities of 155 to 162 Wm^-1K^-1 in a certain direction [24, 27].  Consequently, significant factors for high thermal conductivity are densification, phase transformation, doping of Y₂O₃, and growth as well as alignment of β-Si₃N₄ grains.

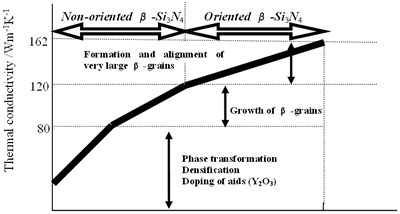
Figure 8. Phenomenal factors shown in the abscissa, which increase the thermal conductivity of Si₃N₄ ceramics.

Thermal Conductivity Data of β -Si₃N₄ Grains

Since it is difficult to synthesize large enough β-Si₃N₄ single crystals for conventional thermal conductive measurements, Li et al. used thermoreflectance microscopy to measure the thermal conductivity of a β-Si₃N₄ single crystal, elongated grain (mean diameter : 17 μm and length: 100 μm) in a ceramic material [14].  Thermal reflectometry is a technique, which relies on local change of reflection coefficient relating to temperature change in a heated sample [40].  The results of this measurement showed that heat flow was more significant along the c-axis of β-Si₃N₄ grains, implying thermal anisotropy in the grain.  The principal thermal diffusivities obtained were 0.84 and 0.32 cm²s^-1 along the c-axis and a-axis, respectively.  The corresponding thermal conductivities, calculated from the density and specific heat of β-Si₃N₄, and experimental thermal diffusivity, were 180 and 69 Wm^-1K^-1 along the c- and a-axis, respectively [14].

Thermal Conduction Mechanisms of β -Si₃N₄ Ceramics

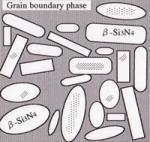
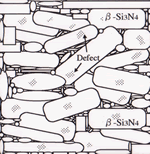
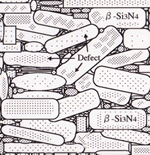
It is important to discuss significant factors controlling the conductivity. Figure 9 indicates possible thermal conduction models of β-Si₃N₄ ceramics, when grain boundary amount and defect density in grains are varied.  In the case of ceramics with a large amount of glassy phase, the thermal conductivity is determined by volume of glassy phase (case I), since thermal conductivity of SiO₂-based glass as grain boundary phase is low (1 Wm^-1K^-1).  For ceramics containing a small amount of grain boundary phase and grains with very few crystal defects, the thermal conductivity is controlled by phonon - grain boundary scattering (case II).  On the other hand, for ceramics containing a small amount of glassy phase and grains with a large amount of crystal defects, their thermal conductivity is greatly influenced due to quantity of crystal defects (case III).  The amount of grain boundary phase of conventional β-Si₃N₄ ceramics is less than 10 vol% [25], suggesting cases II and III as possible thermal conduction models of conventional Si₃N₄ ceramics.

In order to understand the density of crystal defects in the grains, it is significant to compare difference between the intrinsic conductivity and experimental conductivity of grains.  Reported thermal conductivity of a very large elongated β-Si₃N₄ grain was 180 Wm^-1K^-1 along the c-axis [14].  This value is 56% for the predicted intrinsic conductivity (320 Wm^-1K^-1) of β-Si₃N₄, indicating a large amount of crystal defects into the grains.  Consequently, thermal conduction mechanism of recently developed β-Si₃N₄ ceramics is close to the case (III) model.

Kitayama et al. postulated in their paper that thermal conductivity of β-Si₃N₄ grains is 180 Wm^-1K^-1 [41].  Hirosaki et al. did not take account of thermal conductivities of β-Si₃N₄ grains with various sizes, and concentrated on the grain growth only [21].  Therefore, they concluded that thickness of grain boundary and grain size (number of two-grain junctions) are significant factors determining conductivity.  But, grain size does not influence strongly the conductivity in a broad range, as shown in Figure 6.  For instance, the conductivities of specimens with mean grain sizes of 6 and 11 μm with 3 mol% Y₂O₃ addition were almost equal.  In the case of Al₂O₃ and Al₂O₃-Y₂O₃ additions, no change of the conductivities was observed with increasing grain size.  On the other hand, since total aid content determines thickness of grain boundary phase, the lower the amount of sintering aid the higher thermal conductivity obtained.  However, conductivities of specimens with 0.5 mol% additives in the Y₂O₃-Nd₂O₃ and Y₂O₃-Al₂O₃ systems are lower than those of specimens with 1 mol% additives, as shown in Figure 5.  It is considered from these experimental results that thermal conduction of β-Si₃N₄ ceramics sintered with low amount of additives may not be strongly influenced by the thickness of grain boundary and grain size.

Controlling Factors on the Conductivity

Crystal Defects into β-Si₃N₄ Grains

From above discussion, crystal defects into the β-Si₃N₄ grains is one of the significant factors on the conductivity.  Several reports concerning dislocations into Si₃N₄ grains have been published [42-46].  Brito et al. observed the microstructure of β-grains of a specimen with a room temperature conductivity of 120 Wm^-1K^-1, and found dislocations and strong strain contrast inside the grains [43, 44].

Solid solution may also affect the conductivity.  Two possible processes to form the solid solution have been proposed.  One depends on the type of sintering aids.  Addition of Al₂O₃ results in Si₃N₄ solid solution (SIALON) [47, 48].  Aluminum and oxygen in Si₃N₄ turn out to be substitutional impurities in the crystal.  Oxygen replaces nitrogen, and aluminum replaces silicon.  In this case, mass differences and vacancies form in lattices, and they act as phonon scattering sites [19].  Therefore, conductivity of Al₂O₃-doped β-Si₃N₄ ceramics is always low, and is less than 30 Wm-1K-1 [19].  Other possible process is due to solution-reprecipitation process of liquid-phase sintering.  Hirosaki et al. observed the internal structure of β-Si₃N₄ grains in a ceramic with Y₂0₃-Nd₂O₃ additives not to form solid solutions, and found amorphous particles of 5 nm in size, and crystalline Y-Nd-apatite ( (Y,Nd)₁₀Si₆O₂₄N₂ ) particles of 10-30 nm in diameter  in the Si₃N₄ grains, which are presumably formed during cooling by the precipitation of Y-Nd-SiO-N [49].  Besides the crystal defects described above, change of crystal structure has been observed in β-Si₃N₄ grains, although the specimens were fired at ultra-high temperature.  Munakata et al. annealed β-Si₃N₄ grains under a firing condition of 2200°C and 30 MPa in N₂, and observed the existence of α-type structure in β-Si₃N₄ grains by transmission electron microscopy [46].  Point defects may be significant [25, 30].  Very recently, Kitayama et al. have succeeded in measuring the oxygen content in the β- Si₃N₄ crystal lattices by the hot-gas extraction method, and found that β-Si₃N₄ has oxygen contents of 0.158-0.258% depending on additive compositions [50].  Furthermore, they applied electron spin resonance (ESR) to measure the amount of vacancies in the β-Si₃N₄ grains, and detected nitrogen vacancies, which were associated with dissolved oxygen atoms [51].

Phonon Mean Free Path

In the case of nonmetallic solids such as β-Si₃N₄, heat transfer is dominated by phonon transport. Experimental thermal conductivity (κ) is given by :

κ =  C x V x λ / 3           (2)

where C is the heat capacity, V the group velocity and λ is phonon mean free path [52].  Here, phonon mean free path of β-grain with a value of 180 Wm^-1K^-1 [14] is calculated using equation (2) with reported values of group velocity and heat capacity [10, 19], and is estimated to be ~36 nm. The length is much smaller than the grain size, and is much larger than the β-Si₃N₄ a-axis and c-axis lattice parameters (0.761 and 0.291 nm, respectively).  The calculated distance is, therefore, considered to correspond to the interval of crystal defects, i.e. point defects and dislocations.  The authors have been focusing their attention on point defects, because the number of point defects inside grains is much larger than the number of dislocations.  Among the type of point defects, dissolved oxygen atoms have been found into β-Si₃N₄ grains as mentioned above.  This may be a significant factor influencing the conductivity.  To understand the relationship between internal defects and thermal conductivity quantitatively, further works must be conducted focusing on microstructural characterization of grains and precise chemical analysis of the impurities in grains.

Grain Size

According to the previous section, grain size do not influence the conductivity of β-Si₃N₄ ceramics, however type and density of crystal defects in the grains determine the conductivity.  Especially, for the case of Al₂O₃ addition, since Al₂O₃ produces Si₃N₄ solid solution, so effects of grain size on the conductivity was not observed as shown in Figure 6.  On the other hand, Y₂O₃-doped specimens show increase of conductivity with increasing grain size.  Brito et al. observed internal structure of β-grains of Y₂O₃-doped specimen with a conductivity of 122 Wm^-1K^-1, and found that smaller grains have higher defect density, suggesting that thermal conductivity of smaller grains is lower.  For this reason, in the case of Y₂O₃ addition, grain growth produces high conductivity.  So, the increasing thermal conductivity with increasing the grain size for Y₂O₃ addition is not due to the increase of grain size, but is due to removal of crystal defects.

Thermal Anisotropy

Anisotropic thermal conductivity in the β-Si₃N₄ ceramics should be noted.  Hirao et al. [23], Watari et al. [24], and Akimune [27] found thermal anisotropy of highly oriented Si₃N₄, and they mentioned that direction of β-grain orientation shows much higher conductivity compared to other directions.  On the other hand, Li et al. established that the conductivity along the c-axis of β-Si₃N₄ is about three times higher than the conductivity along the a-axis [14].  Thus, it is considered that anisotropic conductivity of highly oriented β-Si₃N₄ is closely associated with the intrinsic and anisotropic conductivity of β-Si₃N₄ grains depending on the crystal axis.  Consequently, orientation and aspect ratio of β-Si₃N₄ grains are key factors affecting the conductivity.

Y₂O₃ Additive

Microstructural observation shows that Y₂O₃ additive is localized as an yttrium-silicon oxynitride crystalline or glassy phase at triple-grain junctions or intergranular glassy film [53, 54].  No significant change of lattice parameters of β-Si₃N₄ has been observed when Y₂O₃ additive is employed [48].  Furthermore, yttrium-silicon oxynitride, accommodates appreciable quantities of transition and alkali impurity elements contained in raw powders into grain boundary phases, and minimizes soluble impurities into grains [54].  Consequently, addition of this aid does not produce point defects such as vacancies, interstitial atoms, substitutional atoms and solid solutions, and increases thermal conductivity of β-Si₃N₄ ceramics.

Conclusions

Experimental observations and theoretical calculations show that the amount and type of crystal defects in grains as well as thermal anisotropy are significant factors on the conductivity of β-Si₃N₄ ceramics.  Removal of crystal defects in grains is an important factor to increase thermal conductivity of β-Si₃N₄ ceramics, and is achieved by using high purity powders, selection of effective sintering aids and controlling grain growth.  Increasing thermal anisotropy in β-Si₃N₄ ceramics is also achieved by grain orientation during forming. Combination of these process techniques produces β-Si₃N₄ ceramics with higher thermal conductivities than 150 Wm^-1K^-1 at room temperature.

Acknowledgements

We would like to thank Prof. K. Mori of Toyama University for some thermal conductivity measurements and useful discussions.  Thanks are also extended to Drs. L.Pottier, B-C. Li and J. P. Roger, and Prof. Dr. D. Fournier for Laboratoire d'Instrumentation de l'Universite Pierre et Marie curie for very useful measurements of local thermal conductivity of Si₃N₄ grains and valuable comments.  In addition, the authors are grateful to Dr. S. Kanzaki of National Institute of Advanced Industrial Science and Technology and Dr. M. Kitayama of Synergy Ceramics Laboratory, Fine Ceramics Research Association (presently, Fukuoka Institute of Technology), for valuable comments and discussion on this work.

References

1.     D. Hardie and K. H. Jack, “Crystal Structure of Silicon Nitride”, Nature, 180 (1957) 332-335.

2.     P. F. Becher, “Microstructural Design of Toughened Ceramics”, J. Am. Ceram. Soc., 74 (1991) 255-269.

3.     M. Yoshimura, T. Nishioka A. Yamakawa and M.Miyake, “Grain Size Controlled High-strength Silicon Nitride Ceramics”, J. Ceram. Soc. Japan, 103 (1995) 407-409.

4.     N. Kondo, Y. Suzuki and T. Ohji, “Superplastic Sinter-forging of Silicon Nitride with Anisotropic Microstructure Formation”, J. Am. Ceram. Soc., 82 (1999) 1067-1069.

5.     T. Kawashima, H. Okamoto, H. Yamamoto and A. Kitamura, “Grain Size Dependence of the Fracture Toughness of Silicon Nitride”, J. Ceram. Soc. Japan, 99 (1991) 320-323.

6.     K. Hirao, T. Nagaoka, M. E. Brito and S. Kanzaki, “Microstructure Control of Silicon Nitride by Seeding with Rodlike β-silicon Nitride Particles”, J. Am. Ceram. Soc., 77 (1994) 1857-1862.

7.     G. A. Slack, “Non-metallic Crystals with High Thermal Conductivity”, J. Phy. Chem. Solids, 34 (1973) 321-335.

8.     G. A. Slack, R. A. Tanzilli, R. O. Pohl and J. W. Vandersande, “The intrinsic Thermal Conductivity of AlN”, ibid., 48 (1987) 641-647.

9.     C. L. Julian, “Theory of Heat Conduction in Rare-Gas Crystals”, Phys. Rev., 137 (1965) 128-136.

10. K. Watari, Y. Seki and K. Ishizaki, “Temperature Dependence of Thermal Coefficients for HIPed Silicon Nitride”, J. Ceram. Soc. Japan, 97 (1989) 174-181.

11. G. A. Slack and I. C. Huseby, “Thermal Gruneisen Parameters of CdAl₂O₄, β-Si₃N₄, and other Phenacite-type Compounds”, J. Appl. Phys., 53 (1982) 6817-6822.

12. K. Watari, B-C. Li, L. Pottier, D. Fournier and M. Toriyama, ”Thermal Conductivity of Beta-Si₃N₄ Single Crystal”, Key Engineering Materials, 181 (2000) 239-242.

13. J. S. Haggerty and A. Lightfoot, “Opportunities for Enhancing the Thermal Conductivities of SiC and Si₃N₄ Ceramics Through Improved Processing”, Ceram. Eng. Sci. Proc., 16 (1995) 475-487.

14.  B-C. Li, L. Pottier, J. P. Roger, D. Fournier, K. Watari and K. Hirao, “Measuring the Anisotropic Thermal Diffusivity of Silicon Nitride Grains by Thermoreflectance Microscopy”, J. Euro. Ceram. Soc., 19 (1999) 1631-1640.

15. M. Kuriyama, Y. Inomata, T. Kijima and Y. Hasegawa, “Thermal Conductivity of Hot-pressed Si₃N₄ by the Laser Flash Method”, Am. Ceram. Soc. Bull., 57 (1978) 1119-1122.

16. K. Tsukuma, M. Shimada and M. Koizumi, “Thermal Conductivity and Microhardness of Si₃N₄ with and without Additives”, Am. Ceram. Soc. Bull., 60 (1981) 910-912.

17. G. Ziegler and D. P. Hasselman, “Effect of Phase Composition and Microstructure on the Thermal Diffusivity of Silicon Nitride”, J. Mater. Sci., 16 (1981) 495-503.

18. K. Hayashi, S. Tsujimoto, T. Nishikawa and Y. Imamura, “Thermal Conductivity of Reaction Bonded Si₃N₄”, J. Ceram. Soc. Japan, 94 (1986) 595-600.

19. K. Watari, Y. Seki and K. Ishizaki, “Thermal Properties of HIPed Sintered Silicon Nitride”, J. Ceram. Soc. Japan, 97 (1989) 56-62.

20. C.W. Li, J. Yamanis, P. J. Whalen, C. J. Gasdaska and C. P. Ballard, “Properties of in Situ Reinforced Silicon Nitride Ceramics”, Mater. Res. Soc. Symp. Proc., 251 (1992) 103-111.

21. N. Hirosaki, Y. Okamoto, M. Ando, F. Munakata and Y. Akimune, “Effect of Grain Growth on the Thermal Conductivity of Silicon Nitride”, J. Ceram. Soc. Japan, 104 (1996) 49-53.

22. N. Hirosaki, Y. Okamoto, M. Ando, F. Munakata and Y. Akimune, “Thermal Conductivity of Gas-pressure Sintered Silicon Nitride”, J. Am. Ceram. Soc., 79 (1996) 2978-2982.

23. K. Hirao, K. Watari, M. E. Brito, M. Toriyama and S. Kanzaki, “High Thermal Conductivity in Silicon Nitride with Anisotropic Microstructure”, J. Am. Ceram. Soc., 79 (1996) 2485-2488.

24. K. Watari, K. Hirao, M. E. Brito, M. Toriyama and S. Kanzaki, “Hot Isostatic Pressing to Increase Thermal Conductivity of Si₃N₄”, J. Mater. Res., 14 (1999) 1538-1541.

25. K. Watari, K. Hirao, M. Toriyama, and K. Ishizaki, “Effect of Grain Size on the Thermal Conductivity of Si₃N₄”, J. Am. Ceram. Soc., 82 (1999) 777-779.

26. N. Hirosaki, Y. Okamoto, F. Munakata and Y. Akimune, “Effect of Seeding on the Thermal Conductivity of Self-reinforced Silicon Nitride”, J. Euro. Ceram. Soc., 19 (1996) 2183-2187.

27. Y. Akimune, F. Munakata, K. Matsuo, N. Hirosaki, Y. Okamoto and K. Misono, “Raman Spectroscopic Analysis of Structural Defects on Hot Isostatically Pressed Silicon Nitride”, J. Ceram. Soc. Japan., 107 (1999) 339-342.

28. K. Watari, M. E. Brito, M. Toriyama, K. Ishizaki, S. Cao and K. Mori, “Thermal Conductivity of Y₂O₃-Doped Si₃N₄ Ceramics at 4 to 1000K”, J. Mater. Sci. Letters, 18 (1999) 865-67.

29. N. Hirosaki, M. Ando, Y. Akimune and M. Mitomo, “Gas-pressure Sintering of β-silicon Nitride Containing Y₂O₃ and Nd₂O₃”, J. Ceram. Soc. Japan, 100 (1992) 826-829.

30. K. Watari, K. Hirao, M. E. Brito and M. Toriyama, Abstract of 1997 the 4th IUMRS (International Union of Materials Research Societies) International Conference in Asia, pp. 477, Paper #. L 4.2, Chiba, Japan, Sep. 16-18 (1997).  

31. T. Nakamatsu, N. Saito, Ch. Ishizaki and K. Ishizaki, “Surface Characterization of Aqueous Washed Silicon Nitride Powders by TPDMS and Isoelectric Point Measurement”, Scripta Mat., 44  (2001) 2347-2351.

32. T. Nakamatsu, N. Saito and K. Ishizaki, “Effects of Manufacturing Process on the H₂ and N₂ Evolution of Si₃N₄ Powder Surfaces when Heated up to 1450 ^oC under Ultra High Vacuum Conditions” Advances in Technology of Materials and Materials Processing Journal (ATM), 2 [1] (2000) 42-53.

33. Tran Thi T. H., Ch. Ishizaki and K. Ishizaki, “NHx/OH Surface Groups in Commercial Si3N4 powders Analyzed by Diffuse Reflectance Infrared Fourier Transform (DRIFT) Spectroscopy”, J. of Ceram. Soc. Jpn., 111 [1] (2003) 28-32.

34. Tran Thi T. H., Ch. Ishizaki, K. Ishizaki, “SiHx Absorbance Bands in Si₃N₄ Powder Surfaces Analyzed by Diffuse Reflectance Infrared Fourier Transformation Spectroscopy”, J. of Ceram. Soc. Jpn., 112 [1] (2004) 1-5.

35. Tran Thi T. H., Ch. Ishizaki and K. Ishizaki, “Surface Stracture of Commercial Si3N4 Powder Analyzed by X-ray Photoelectron Spectroscopy (XPS)”, J. of Ceram. Soc. Jpn., accepted, (2005).

36. K. Negita, “Effective Sintering Aids for Si₃N₄ Ceramics”, J. Mater. Sci. Letters, 4 (1985) 755-758.

37. T. Yamada, “Preparation and Evaluation of Sinterable Silicon Nitride Powder by Imide Decomposition Method”, Am. Ceram. Soc. Bull., 72 (1993) 99-106.

38. M. Asayama, K. Nishida, A. Tsuge, S. Kanzaki, T. Ohji, K. Watari, K. Isozaki and H. Hirotsuru, “The Effect of Amount of Halogen Impurities on High Temperature Mechanical Properties of Sintered    Si_３N₄”, Ceramic Transaction, 44 (1995) 325-330.

39. K. Watari, M. Kawamoto and K.Ishizaki, “Evaluation of Carbon Behavior in HIPed Silicon Nitride”, J. Ceram. Soc. Japan, 96 (1988) 760-767.

40. L. Pottier, “Micrometer Scale Visualization of Thermal Waves by Photoreflectance Microscopy”, Appl. Phy. Lett., 64 (1994) 1618-1619.

41. M. Kitayama, K. Hirao, M. Toriyama and S. Kanzaki, “Thermal Conductivity of β- Si₃N₄ I. Effect of Various Microstructural Factors”, J. Am. Ceram. Soc., 82 (1999) 3105-3112.

42. W.E Lee and G. E. Hilmas, “Microstructural Changes in β-silicon Nitride Grains upon Crystallizing the Grain-boundary Glass”, J. Am. Ceram. Soc., 72 (1989) 1931-1937.

43. M. E. Brito, K. Hirao, M. Yasuoka and S. Kanzaki, “Development of High Quality β- Si₃N₄ Rodlike Crystals –characterization by Transmission Electron Microscopy”, Reports on Government Industrial Research Institute, Nagoya, 42 (1993) 7-12. 

44. M. E. Brito, K. Hirao, K. Watari and S. Kanzaki, presented at 1996 Annual Meeting & Exposition of American Ceramics Society (Paper No., SVII-40-96), Indianapolis, U.S.A., April 14-17, 1996.

45. M. E. Brito, K. Hirao, K. Watari, M. Toriyama and S. Kanzaki, submitted to J. Appl. Phy.

46. F. Munakata, C. Sato, N. Hirosaki, M. Tanimura, Y. Akimune, Y. Okamoto and Y. Inoue, “Annealing Effects for Structural Defects of Silicon Nitride Ceramics”, J. Ceram. Soc. Japan, 105 (1997) 858-861.

47. S. Hampshire, H.K. Park, D. P. Thompson and K. H. Jack, “α’-sialon Ceramics”, Nature, 274 (1978) 880-882.

48. A. Tsuge and K. Nishida, “High Strength Hot-pressed Si₃N₄ with Y₂O₃ and Al₂O₃ Addition”, Am. Ceram. Soc. Bull., 57 (1978) 424-431.

49. N. Hirosaki, T. Saito, F. Munakata, Y. Akimune and Y. Ikuhara, “Transmission Electron Microscopy Observation of Second-phase Particles in β- Si₃N₄ Grains”, J. Mater. Res., 14 (1999) 2959-2965.

50. M. Kitayama, K. Hirao, A. Tsuge, M. Toriyama and S. Kanzaki, “Oxygen Content in β- Si₃N₄ Crystal Lattice”, J. Am. Ceram. Soc., 82 (1999) 3263-3265.

51. M. Kitayama, K. Hirao, A. Tsuge, K. Watari, M. Toriyama and S. Kanzaki, “Thermal Conductivity of β-Si₃N₄ II. Effect of Lattice Oxygen,” J. Am. Ceram. Soc., 83 (2000) 1985-1992.

52. J. M. Ziman, "Electrons and Phonons", Oxford University Press, U.K. (1960), Chapter VIII.

53. A. Tsuge, H. Inoue and K. Nishida, “Grain-Boundary Phase Characterization of Silicon Nitride with Material Loss during Heat Treatment”, J. Am. Ceram. Soc., 72 (1989) 2014-2016.

54. D. R. Clark and G. Thomas, ”Microstructure of Y₂O₃ Fluxed Hot-pressed Silicon Nitride”, ibid., 61 (1978) 114-118

Contact Details

Koji Watari

National Institute of Advanced Industrial Science and Technology
Ceramics Research Institute
Shimo-Shidami, Moriyama-ku
Nagoya 463-8560
Japan

E-mail: [email protected]

Kiyoshi Hirao

National Institute of Advanced Industrial Science and Technology
Synergy Material Center
Shimo-Shidami, Moriyama-ku
Nagoya 463-8687
Japan

Manuel E. Brito

National Institute of Advanced Industrial Science and Technology
Synergy Material Center
Shimo-Shidami, Moriyama-ku
Nagoya 463-8687
Japan

Motohiro Toriyama

National Institute of Advanced Industrial Science and Technology
Ceramics Research Institute
Shimo-Shidami, Moriyama-ku
Nagoya 463-8560
Japan

Kozo Ishizaki

Department of Mechanical Engineering, Nagaoka University of Technology
940-2188, Niigata
Japan

This paper was also published in print form in “Advances in Technology of Materials and Materials Processing”, 7[2] (2005) 191-202.