Measuring Voltages in Optical Quantum Computers

By Surbhi JainJun 13 2022Reviewed by Susha Cheriyedath, M.Sc.

In an article recently published in the open-access journal Energies, researchers discussed the voltage measurement with high precision for optical quantum computation.

Study: High-Precision Voltage Measurement for Optical Quantum Computation. Image Credit: Bartlomiej K. Wroblewski/Shutterstock.com

Background

Quantum events that occur in optical systems can be used to do quantum computation and communication. There are quantum computer implementations that do not exclusively rely on optical processes but rather on atom-light interaction. The fundamental issue with such a method is the requirement to cool the system to a very low temperature, which does not apply to optical quantum systems. Using entangled photon sources like thin films or quantum dots can boost source efficiency.

Practical applications necessitate a thin-film-based source of entangled photons. When the number of qubits and quantum volume is increased, scaling concerns occur. Due to their huge size and greater need for precision, optoelectronic devices cannot have significant values of these characteristics. Photonic chips, on the other hand, can solve these issues. The measurement of voltage across the photodiode sensors that terminate the optical system is a critical component of all approaches. There are two types of voltage measurements: photoconductive and photovoltaic.

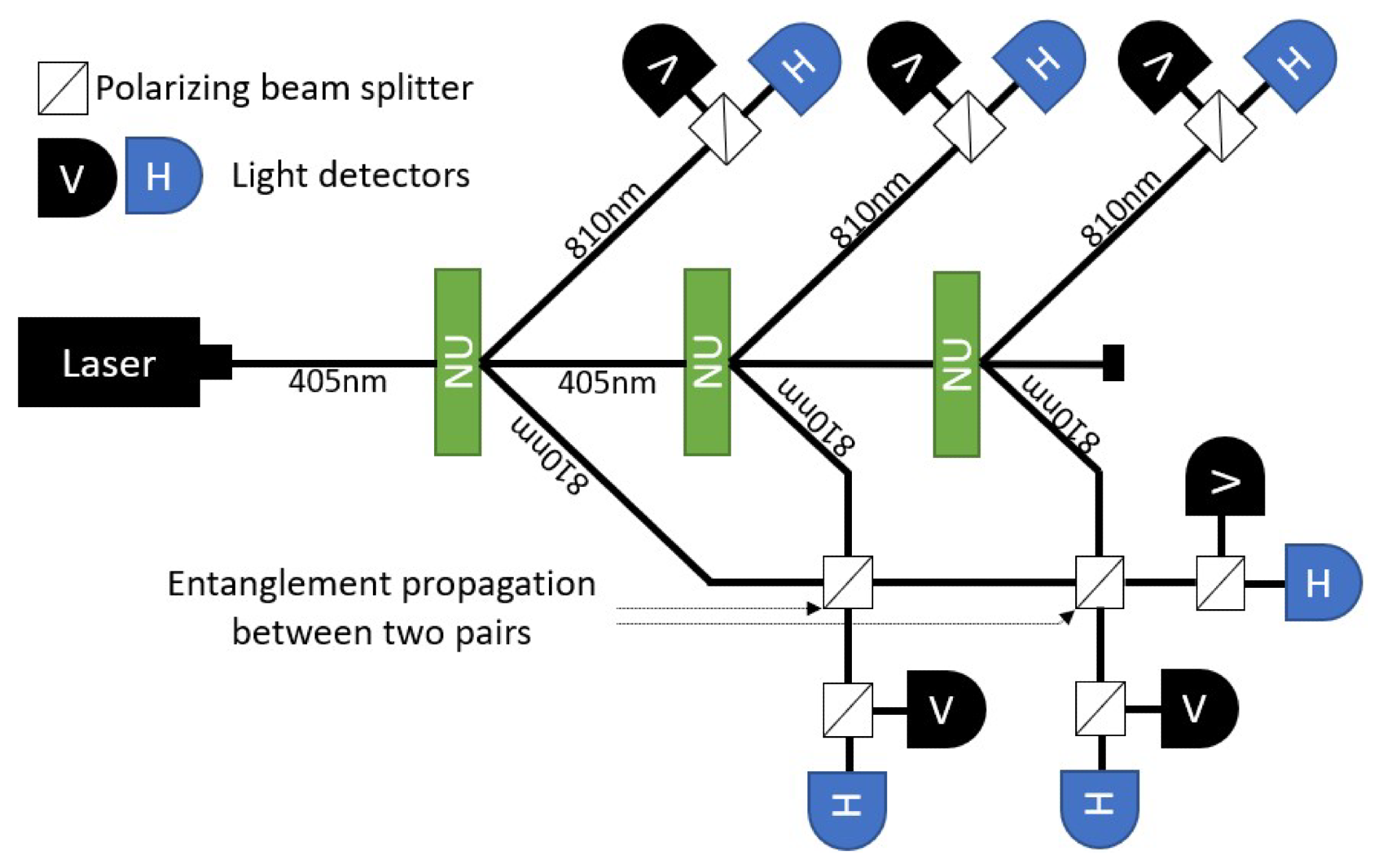
Experimental setup for six-photon entanglement. Firstly, two pairs of photons are generated by nonlinear units (NUs) in series. Following this, one photon from each pair reconnects with the remaining section of the system via the polarization beam splitter. From the reconnection points, entanglement propagates throughout the entire system, generating the GHZ state. Image Credit: Wereszczy´nski, K. et al., Energies

About the Study

In this study, the authors presented a theoretical investigation on the utilization of optical systems for quantum computation. An optical superstructure capable of implementing specified compute algorithms and operations was developed. Nonlinear optical units like beta barium borate crystals were used to make up the superstructure.

The units were connected in series and powered by a pulse laser pump, and the output state of the entangled photon pairs was generated by a beam splitter. Entanglement propagation using beam splitters and configurable phase shifters, which set associated parameters, was used to compute.

The team demonstrated how a succession of cosine-based components could be built using a two-component case. The optical phenomena involved in the quantum computation were given a quantum description. The optical setup and quantum computation protocols were also presented. Photodiode photon-to-voltage converters, optional amplifiers, and a coincidence counter made up the experimental setup.

The researchers presented a novel concept for the implementation of quantum computation utilizing optical devices. The distortion of a homogeneous distribution of probability over optical detectors produced by phase changes between rails was employed in the implementation. The implementation of one part of the cosine-series-sampled operator QCoSamp was demonstrated.

Diagram of (left) the beam splitter and (right) the polarization beam splitter, acting on the two-rail states with polarization. Image Credit: Wereszczy´nski, K. et al., Energies

Observations

The segment of the optical path that creates a single QCoSamp component, as well as the mechanism for adding more components, must be identified. The components, however, were not precisely demarcated due to the nature of the proposed system. The beam splitters applied to the MOS output and the attached phase shifters roughly identified a single component. The argument of the component could be changed by altering the phase of the phase shifters.

More nonlinear units, as defined in the preceding section, could be used to incorporate more components. The entanglement was propagated further as a result of this augmentation. Algorithms like amplitude amplification must iterate numerous times utilizing the same gates. This could be accomplished by creating a loop in the light pathway, thus boosting the quantum volume of such devices without the requirement of the implementation of numerous extra gates. Because entanglement was used as a resource for quantum computation, as well as a tool for generating control gates via entanglement between qubits, the suggested implementation using optical quantum phenomena had no issues. Entanglement allowed a change in the phase of one rail via the phase shifter of another rail.

A high-efficiency entangled photon source, such as ultra-thin films or quantum dots, could be used to compensate for the loss of efficiency. Signal processing, feature extraction, image processing, and image classification techniques could all be implemented on photonic circuits using the proposed architecture. Furthermore, the described arrangement provided extra output options. The detection of four or more photons in two polarization states had a temporal connection. The ququartits' states necessitated a special detector in the proposed arrangement. The state |00> must be discovered by observing the rest of the system. However, states like |20>, which had two photons on the same rail with the same polarization, were excluded because they were not needed for computations.

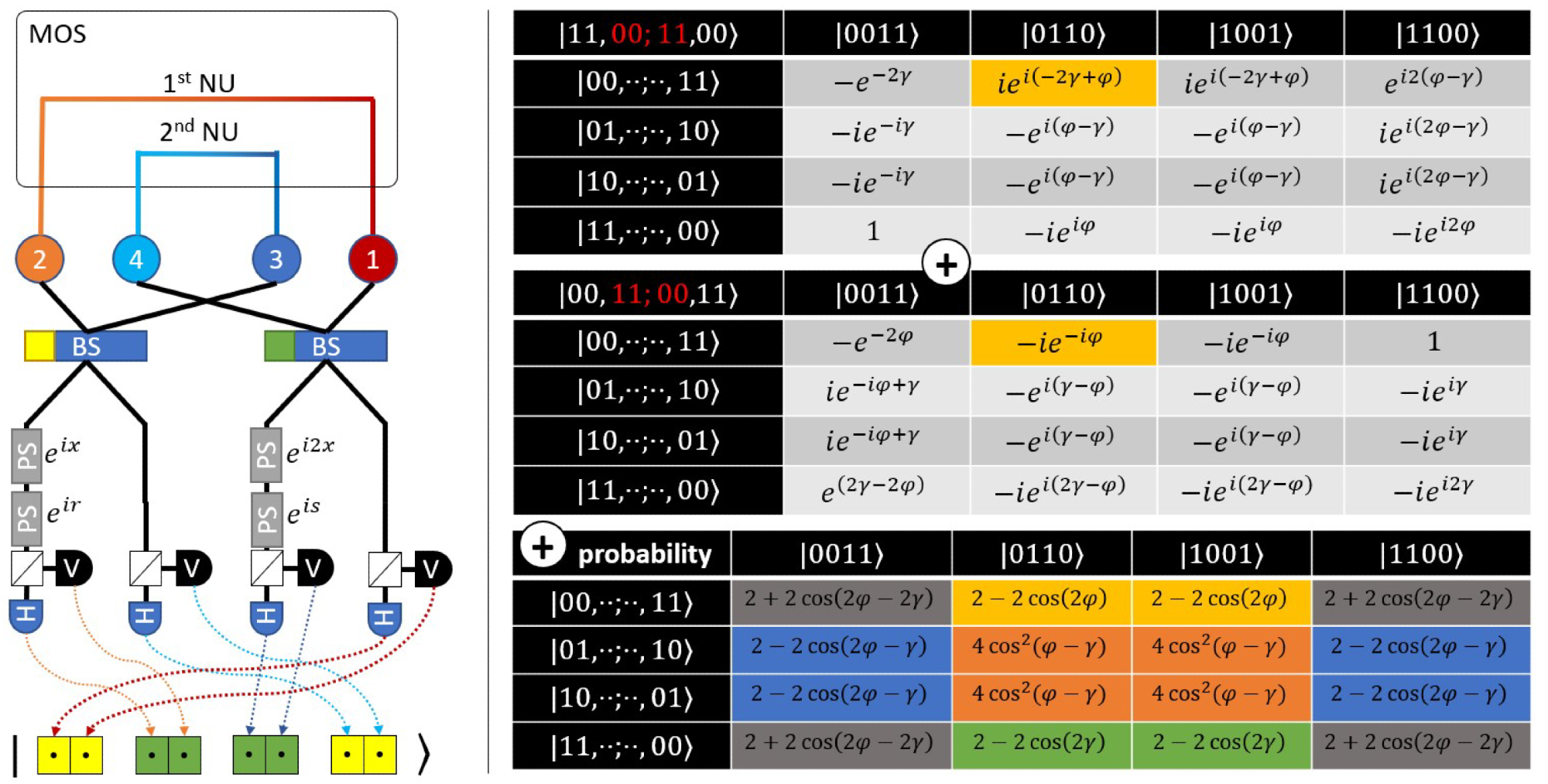
Diagram showing (left) the optical path and (right) the tables of coefficients for the two states corresponding to the path. Image Credit: Wereszczy´nski, K. et al., Energies

Conclusions

In conclusion, this study elucidated the development of an optical setup that provided a single component for the QCoSamp operator. The authors also demonstrated how the addition of additional components could generate a series. The amplitude amplification algorithm, which is at the heart of the optimization approaches available in QCoSamp, was implemented.

The team mentioned that the findings of this study are relevant to quantum sampling and quantum communication, and they serve as a foundation for further research and the creation of physical implementation.

They also stated that future research should look into building a quantum optimizer using quantum sampling methods, as well as high-precision temporal voltage measurement, which is a crucial procedure in the construction of high-fidelity devices.

Source

Wereszczy´nski, K., Michalczuk, A., Paszkuta, M., et al. High-Precision Voltage Measurement for Optical Quantum Computation. Energies 15(12) 4205 (2022). https://www.mdpi.com/1996-1073/15/12/4205

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.