Introduction The local microstructure of amorphous material has been the subject of numerous studies [1-8]. Of great interest are pores and clusters formed by several pores that are responsible for unusual properties not observed in a crystal. Some researchers assumed that the existence of large pores in amorphous solid was improbable. However, the latest simulation indicated these pores are fairly stable. Experimental studies by positron annihilation, small angle X-ray scattering and electron microscopy have already shown that the detected microvoids are similar to vacancies in a crystal. In several real amorphous alloys it was found experimentally these “quasivacancies” combined in clusters. Chan and Elliott [9] calculated the size of pore distribution in an amorphous model of silica constructed by Monte-Carlo method. They found that there were 3.1x1021 pores/cm3 with radii of 1.28 Å (atomic He radius). Similar calculation of size distribution of pores for amorphous metallic models also detected large pores (the radii close to atomic radii) with significant concentrations [4, 6, and 7]. For systems Co-P and Co-B others [4] found that the number of large pores surrounding a phosphorous atom is much larger than one surrounding boron atom. In addition, the number of large pores surrounding a cobalt atom in system Co-P is larger than one surrounding a cobalt atom for system Co-B. Introduction of simple geometric measures that quantify microscopic structural order holds promise for clarifying relationship between structural disorder and physical property. Recently, it were the Voronoi polyhedron, coordination number, bond angle distribution etc., which are useful for identifying the structural inhomogenities of amorphous materials. However, the pores characteristics reported in previous works such as radii distribution and number of pores surrounding central atom can not fully describe the problems of pores yet. Furthermore, due small models (several thousand atoms) it was found that only from a few large pores it is difficult to estimate the diffusion role of these vacancy-like pores. In this work we have done a simulation of microstructure of large amorphous models CoxB1-x to provide the following: i. The size distribution of cluster formed by pores which can be detected only in large models and has not been investigated for amorphous metallic system. ii. Several new local structural characteristics that give additional insight in amorphous structure of system Co-B. iii. Exact concentration of vacancy-like pores. Calculation Method The calculations were carried out for three models Co90B10, Co81.5B18.5 and Co70B30 containing 200,000 atoms in a cubic simulation cell with boundary periodic conditions. Initial states of models were a random arrangement of all atoms in the simulation cell. The density of these models was chosen to be the real density of amorphous alloys. Then systems were relaxed until reaching the new equilibrium state. Final states were accomplished by 20,000 steps of statistic relaxation. In [5] the amorphous alloys CoB is given by the Pak-Doyama potential and the constructed models gain good agreement with the experiments for the partial pair-distribution function (PDF). This potential has the following form: ϕ(r) = a(r-b)4 + c(r-d)2 + e (1) Where r and ϕ(r) are in Å and eV respectively. Potential (1) was cut off in a distance R which is listed in Table 1. Table 1. The parameters of interatomic potential for system Co-B. | | | Co-Co | -0.12812 | -1.82709 | 1.15421 | -2.50849 | -0.134479 | 3.44 | | Co-B | -0.10967 | -1.47709 | 0.98799 | -2.15849 | -0.11511 | 3.09 | | B-B | -0.87724 | -2.17709 | 0.79028 | -2.85849 | -0.09208 | 3.79 | After each run, the PDF and local structural characteristics were calculated. To determine the pores all sets of four neighbour atoms in the model were taken. Two atoms were considered as neighbours if their distance was less than 5.5 Å. Then a sphere was inserted in contact with these spherical atoms. The radii of cobalt and boron atoms set to 1.25 and 0.81 Å respectively. The inserted pore may be overlapped with an atomic sphere or with other pores. For the first case the inserted pore was removed from the system. In the second case the removing of smaller pore will be performed if the distance r between these overlapped pores and their radii r1 and r2 (r1<r2) satisfy following condition: r1 + r2 + r < 2r2 + 0.1r1 (2) The condition (2) allowed retaining the biggest pore and removing from set of overlapped pores, small ones almost located inside a big pore. Based on set of obtained pores, the next step is the calculation of the following parameters: i. The radius distribution of all pores in models f1(r). ii. The size distribution of three items: - for an isolated pore, which did not intersect with any other pores f2(d). - for two overlapped pores f3(d). - for a cluster of more than two overlapped pores f4(d). Figure 1 gives the shape of these three items and shows how to estimate their diameter. They are called as structural defect of A, B and C types respectively. The defect C contains a pore at the center and other smaller pores surrounding it. The diameter of defect C is calculated by averaging diameters of all pores in a defect C. iii. The number distribution of pores surrounding a central atom f5(N) and the number distribution of atoms f6(Z) which are in contact with a central pore. iv. The angular distribution f7(θ), where θ is the angle in a tetrahedron which is created by four atoms in contact with a central pore (see Figure 1). | 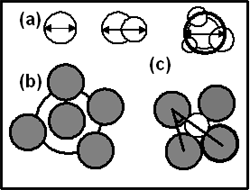
| | Figure 1. (a) The shape of structural defects of types A, B and C. (b) Free volume surrounding a central atom. (c) Tetrahedron formed by four neighbors atoms contains a pore inside. This tetrahedron is used to calculate the angles distribution. Gray circle - atomic sphere, white circle – pore. | An additional characteristic which clarifies the local atomic arrangement is free volume around a central atom as shown in Figure 1. In order to calculate this parameter 10,000 points are inserted randomly inside a sphere located at the center of a central atom with radius Rf equal to 3.4 Å. This radius corresponds to the first minimum of PDF for the pair Co-Co. The free volume around a central atom was determined as V = 4π(Rf)3n / (3*10,000) (3) Where n is number of inserted points that are located outside atomic spheres in the model. For convenience, the non-unit parameter V0 = 3V/4π(Rf)3 =n/10,000 is calculated instead of V. Result and Discussion The PDF of the constructed model Co81.5B18.5 is demonstrated in Figure 2. For other models their PDF has a similar form. Generally, all PDFs of obtained models are close to data reported in [7] for smaller models. Figure 3 displays the calculated total x-ray PDF and compares it to experimental data [10]. We can see that the simulation reproduces experimental data reasonably well. | 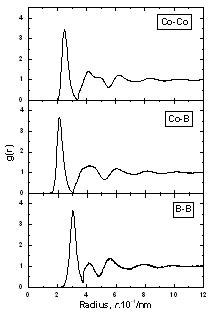
| | Figure 2. The radial distribution function of amorphous model Co81.5B18.5 | | 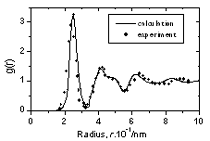
| | Figure 3. The radial distribution function of amorphous model Co81.5B18.5 | The pore radius distribution for system Co81.5B18.5 is shown in Figure 4. There are two peaks. The first peak is located at 0.32Å and the second one at 0.52Å. The number of pores with radius bigger than 0.9Å is 0.00474 pores per atom. The biggest pore has radius equal to 1.38Å. As shown in [1] these large pores can exchange their position with neighbouring atoms and therefore they can play a role of vacancies in the diffusion process. These pores are called as vacancy-like pores. The Table 2 lists the number of large cavities with radii bigger than 0.9 Å and radii of biggest pores found in three models. As listed in Table 2 the system Co70B30 has 0.01468 vacancy-like pores per atom and radii of biggest pore found in them is equal to 1.66 Å. The corresponding values for model Co90B10 are 0.00288 and 1.30 Å respectively. This data indicated that the addition of small atom B destroys the basic amorphous structure and creates new defects in them. 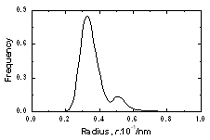
Figure 4. The pore radius distribution of amorphous model Co81.5B18.5 Table 2. Number of large cavities per atom and radii of biggest pore in amorphous alloys. | | | Number of cavities per atom (r> 0.9 Å) | 0.00288 | 0.00474 | 0.01468 | | Radii of biggest pore in a model, Å | 1.30 | 1.38 | 1.66 | Figure 5 presents the size distribution of structural defects of A, B and C types. The splitting in two sub-peaks is not observed here as shown in Figure 4. Therefore the second peak in radius distribution f1(d) is related to more complicated types B or C of defects. The distributions f2(d), f3(d) and f4(d) for amorphous models Co90B10 and Co70B30 are similar to Co81.5B18.5 model. The peaks for distributions of defects A, B and C are located at 0.62, 1.28 and 1.90 Å respectively. Small difference in heights of peaks was obtained. Its values for defect A of Co70B30, Co81.5B18.5 and Co90B10 models are equal to 0.2488, 0.2967 and 0.3229 respectively. Generally, the distribution f2(d) for model with richer boron is spread broader. The Table 3 lists the fraction of all defects formed by pores. It is clear that by increasing the boron concentration in systems leads to decreasing the fraction of defect A, but increases the fraction of defects B and C. The fraction of A defects decreased from 0.7206 to 0.6743 while increasing the boron concentration. In reverse, fraction of C defects containing more two pores increased up from 0.1172 to 0.1484 for the model Co70B30 and model Co90B10. This data also showed the increasing structural disorder with boron addition in systems. 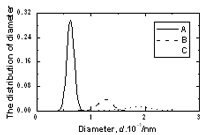
Figure 5. The size distribution of structural defects of types A, B and C in amorphous model Co81.5B18.5 Table 3. The fraction of structural defects in amorphous alloys | | | Co90B10 | 0.7206 | 0.1622 | 0.1172 | | Co81.5B18.5 | 0.7017 | 0.1703 | 0.1281 | | Co70B30 | 0.6743 | 0.1773 | 0.1484 | Important information of local atomic arrangement is provided by angle distribution f7(θ) This angle distribution for system Co81.5B18.5 is shown in Figure 6. The peak of angle distribution is located near 600 that is responsible for the right tetrahedron. In the model of Co70B30 the maximum of curve f7(θ) is located at 550 and it is spread broader than for system Co81.5B18.5. In reverse, model of Co90B10 has sharper peak of f7(θ). It means that the tetrahedron of four neighbor atoms and containing a pore inside (Figure 1) has strongly distorted if it is a large pore inside. | 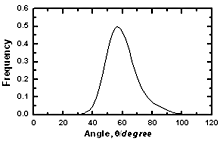
| | Figure 6. The bond angle distribution of amorphous model Co81.5B18.5 | The number of pores surrounding a central atom and number of atoms in contact with pores are distributed in a wide interval ranging from 1 to 25 and 4 to 18 respectively. As shown in Figures 8 and 9 these distributions shift to the right for cobalt atoms in comparison with boron atoms. The averaged number of pores surrounding a central atom is 9 and 15 for B and Co atoms respectively. In comparison with pores in the crystal this value is rather bigger. Therefore, activation mechanism of diffusion along interstices in amorphous alloys may have specific properties in comparison with the crystal. The averaged number of atoms in contact with pore has value of 13 and 9 for Co and B respectively. Analogy to the case of number distribution of pores, the number distribution of atoms also shifts to the right for cobalt in comparison with boron atoms. Some characteristics of distributions f5(N) and f6(Z) are listed in Table 4. | 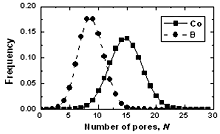
| | Figure 7. The number distribution of pore surrounding a central atom in amorphous model Co81.5B18.5 | Table 4. Characteristics for distributions of number of pores and atoms in contact with a pore. | | | Height of a peak f5(N) for Co atom | 0.1423 | 0.1379 | 0.1307 | | Height of a peak f5(N) for B atom | 0.1817 | 0.1759 | 0.1764 | | Height of a peak f6(Z) for Co atom | 0.2575 | 0.2470 | 0.2282 | | Height of a peak f6(Z) for B atom | 0.3186 | 0.3141 | 0.2815 | | 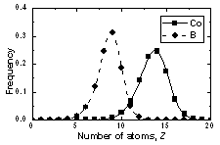
| | Figure 8. The number distribution of atoms in contact with pores in amorphous model Co81.5B18.5 | | 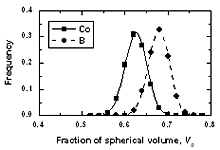
| | Figure 9. The distribution of free volume surrounding a central atom in amorphous model Co81.5B18.5 | Figure 9 depicted the distribution of free volume surrounding an atom. They shift in the right for the boron atom. It can be seen from Figure 8 that the fraction of free volume surrounding boron is rather bigger than that of cobalt atoms. There are about 8% boron atoms with the fraction of free volume surrounding them equal to 0.7. Obviously these places are referred to ‘expanded positions’. For cobalt atom this fraction corresponds to a concentration less than 1%. However there are about 6% cobalt atoms and no more than 1% boron atoms has a fraction of free volume less than 0.5. Hence it is related to ‘compressed positions’. Conclusions The structure of amorphous CoxB100-x models with pair Pak-Doyama potentials is close to the experimental data. There are significant amounts of large vacancy-like pores in these amorphous alloys. The number of such pores is strongly changed with boron concentration. Analyzing the distribution of different kinds of clusters formed by pores, it is found that all vacancy-like pores are involved to the cluster of more than two pores. Approximately estimated diameter of them is rather bigger than the diameter of cobalt atom. Therefore, this structural defect can play a significant role for diffusion in amorphous alloys. The calculation of angle, pore number, atom number and free volume distributions reveals that increasing the boron concentration in system disorders the structure of amorphous alloys. It has been shown that near cobalt atom there are more atoms and pores than around a boron atom. In reverse, fraction of free volume surrounding a boron atom is bigger than one surrounding a cobalt atom. Furthermore, the obtained distribution of free volume also indicated the existence of ‘expanded’ and ‘compressed positions’ in amorphous structure. Acknowledgement Professor D. K. Belashchenko is gratefully acknowledged for useful discussions and comments on the manuscript. References 1. D. K. Belashchenko, “Diffusion mechanisms in disordered systems: computer simulation”, Uspekhi Fizicheskikh Nauk, 42 (4) (1999) 297-319. 2. Daniel J. Lacks, “First-order amorphous-amorphous transformation in silica”, Phys. Rev. Lett., 84 (2000) 4629-4532. 3. M. Scott Shell, G. Pablo, Debenedetti and Athanassios Z. Panagiotopoulos, “Molecular structural order and anomalies in liquid silica”, Phys. Rev.E 66 (2002) 011202-1 - 011202-8. 4. P. K. Hung, P. N. Nguyen and D. K. Belashchenko, “Computer simulation of amorphous alloys Co100-xPx and Co81.5B18.5”, Izv. Akad. Nauk. SSSR, Metally, 2 (1998), 118-121. 5. D. K. Belashchenko, V. V. Hoang, P. K. Hung, “Computer simulation of local structure and magnetic properties of amorphous Co-B alloys”, J. Non-cryst. Solids, 276 (2000) 169-180. 6. V. V. Hoang, T. B. Van and P. K. Hung, “Simulation of structural and magnetic inhomogeneities of amorphous Ni-P alloys”, J. Metast. and Nanocryst. Mater., e-vol 9 (2001) 5-20. 7. V. V. Hoang, N. H. Hung, N. H. T. Anh, “Computer simulation of the effects of B, P concentration on the pore distribution in the amorphous Co-B, Co-P alloys”, J. Metast. and Nanocryst. Mater., e-vol. 18 (2003) 43-48. 8. V. V. Hoang, D. K. Belashchenko, V. T. M. Thuan, “Computer simulation of the structural and thermodynamic properties of liquid and amorphous SiO2”, Phys. B, 348 (2004) 249-255. 9. S. L. Chan., S. R. Elliott, “Theoretical study of the interstice statistics of the oxygen sublattice in vitreous SiO2”, Phys. Rev. B, 43 (1991) 4423-4432. 10. P. Lamparter, E. Nold E., H. Rainer. ”X-ray and neutron diffraction studies on amorphous transition metal-boron alloys (Fe-B, Co-B, Ni-B), Z. Naturforsch, 1981,V.A36,2, 165-171. Contact Details |