Introduction
A photo-control of molecular orientation of polymer materials is of great interest for an optical data storage, birefringent films, highly functionalized optical devices etc [1]. By the use of a linearly polarized light, an optical anisotropy can be generated in polymer films containing a photoactive group, such as azo dye-doped polymers [2, 3], azobenzene-containing polymers [4-6], and anisotropically photoreactive polymer systems [7]. Among them, azo dye-or azobenzene-containing polymers have been extensively studied by many groups in detail. They can induce the optical alignment of the azo group based on trans-cis photoisomerization of the azo units with a direction perpendicular to the electric vector of the linearly polarized light. Alternatively, we studied a photocrosslinkable polymer liquid crystal containing a (cinnnamoyloxy)ethoxybiphenyl side group and its copolymers which exhibit thermally stable reorientation of mesogenic side groups by the use of linearly polarized ultraviolet (LPUV) light and subsequent annealing [8, 9]. The photocrosslinked mesogenic groups were found to realign in the direction parallel to the electric vector of the LPUV light, caused by the axis-selective photoreaction of the cinnamoyl substituent. Additionally, reversion of the in-plane reorientation direction of mesogenic groups has been observed in polymethacrylate liquid crystal films substituted with (4-methoxycinnamoyloxy)biphenyl side group [10]. This means that the reorientation direction can be controlled by the degree of photoreaction.
If the spatial patterns of the molecular reorientation can be designed for the highly functionalized optical devices, the novel types of optical devices can be realized by the use of the controllability of the reorientation direction of the mesogenic molecules. For this purpose, the fabrication technique to realize the reorientation patterns is often emphasized. One of the sophisticated methods is the polarization holographic technique [11-13]. In the polarization holographic technique, two coherent light waves with orthogonal polarization are used as writing beams. The interference pattern of two coherent waves of equal amplitude and orthogonal polarizations (orthogonal linear; OL, and orthogonal circular; OC) has a constant intensity, but it has a polarization state that is periodically modulated in space. If such interference light is irradiated with above-mentioned functionalized materials showing the polarization induced birefringence, the polarization patterns can be recorded in such materials and the preliminary data for the polarization gratings have already been obtained in our previous work [13]. In the present paper, we show one- and two-dimensional polarization gratings stored in our photocrosslinkable polymer liquid crystals and characterize the resulting polarization gratings on the basis of the Jones calculus. The polarization gratings can control both polarization state and propagation direction of the laser beam, and the characteristics were well-explained by the Jones calculus.
Experimental
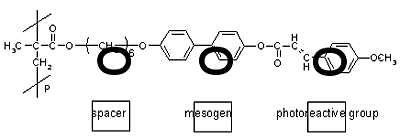
In the present article, we used a photocrosslinkable poly(methyl methacrylate) liquid crystal with 4-(4-methoxycinnamoyloxy)biphenyl side groups as shown in Figure 1 in order to fabricate the thermally stable polarization gratings. The photocrosslinkable polymer liquid crystals were prepared by polymerization of methacrylate monomers utilizing a free radical solution-polymerization in tetrahydrofuran with 2,2’-azobis(isobutyronitrile) as an initiator. According to our previous study, our photocrosslinkable polymer liquid crystal exhibits thermally stable reorientation of mesogenic groups by the use of LPUV light and subsequent annealing. Thin photocrosslinkable polymer liquid crystal films were prepared by spin casting of a solution of the polymer in methylene chloride in clear quarts slides, and the resulted in 300-nm-thick films. The polymer liquid crystal exhibited the amorphous structure and the films showed good optical quality.
|
|
|
Figure 1. Chemical structure of photocrosslinkable polymer liquid crystal.
|
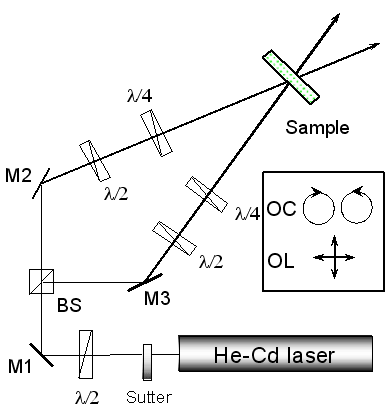
The polarization holographic recordings were conducted with the He-Cd laser which emits continuous wave 325 nm light and the experimental setup is schematically described in Figure 2. The He-Cd laser beam is divided into two writing beams and the two writing beams with equal intensities crossing at the 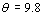 angle impinge upon the polymer liquid crystalline films. The polarization states of the two writing beams were individually controlled by half- and/or quarter wave plates and the polarization gratings were written using two orthogonal polarized, mutually coherent, He-Cd laser beams. The interference pattern of two coherent waves with orthogonal polarizations has a constant intensity, but a polarization state that is periodically modulated. In such a case, if the interference light is irradiated with functionalized materials possessing the laser induced birefringence, the spatially modulated polarization patterns are expected to be recorded on such materials. angle impinge upon the polymer liquid crystalline films. The polarization states of the two writing beams were individually controlled by half- and/or quarter wave plates and the polarization gratings were written using two orthogonal polarized, mutually coherent, He-Cd laser beams. The interference pattern of two coherent waves with orthogonal polarizations has a constant intensity, but a polarization state that is periodically modulated. In such a case, if the interference light is irradiated with functionalized materials possessing the laser induced birefringence, the spatially modulated polarization patterns are expected to be recorded on such materials.
|
|
|
Figure 2. Experimental setup for polarization holographic recording.
|
Theory
In the present article, we consider the effect of two types of polarization interference patterns formed by the interaction of two plane waves E1 and E2, of equal amplitude E and orthogonal polarizations. In the case of OL exposure, E1 is vertical-linearly polarized, while E2 horizontal-linearly polarized, and the resulting two waves are linear-polarized waves with mutually perpendicular polarization directions. The resulting light field (E=E1+E2), is described for the OL case by
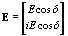 (1) (1)
where the phase difference between the two incident waves δ is a function of the position x and of the grating spacing Λ, and can be expressed as
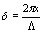 (2) (2)
In the case of OC exposure, E1 and E2 are left- and right-circularly polarized waves. The resulting light field, is described for the OC case by
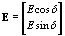 (3) (3)
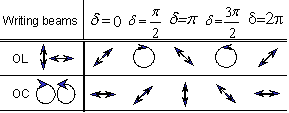
According to equations (1) and (3), Figure 3 summarizes the polarization states of the two writing beams, and the resulting electric field and intensity distribution of the two beams coupling for each irradiation mode.
|
|
|
Figure 3. Types of polarization modulation in recording with two waves with orthogonal polarization.
|
We assume that only linear birefringence is induced in the polarization-sensitive material. In the case of OL exposure, the intensity of the interfering field is constant and only changes in the resultant polarizations among linear, elliptical, and circular states are effective as shown in Table 1. The characteristic ellipsoid does not change the direction of its principal axes but only its ratio. The Jones matrix describing the transmission of the recorded holograms has the form
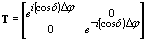 (4) (4)
where Δφ=πΔnd / λ, Δn is the photoinduced birefringence, dis the film thickness, and λ is the wavelength of the reading beam. The Jones matrix describing the holographic recording in the case of OC exposure is
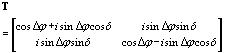 (5) (5)
for phase recording. In order to determine the polarization properties of the reconstructing light wave from the polarization holograms described by Equations (4) and (5), we consider the light field 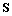 diffracted from them, given by diffracted from them, given by
S = T R (6)
where 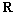 is the reading beam. The polarization of is the reading beam. The polarization of 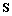 depends on the polarization of depends on the polarization of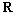 . Figure 4 schematically describes the polarization properties of the reconstructing light on varying the polarization state of the reading beam. . Figure 4 schematically describes the polarization properties of the reconstructing light on varying the polarization state of the reading beam.
|
|
|
Figure 4. Schematics of the polarization conversion by polarization holographic gratings.
|
Results and Discussion
The diffraction was almost invisible for all samples after irradiating with the LPUV interference light, while the samples were annealed at the liquid crystal temperature of 150°C. The grating was thereupon thermally organized and the diffraction spot appeared. The grating was quite stable in ambient atmosphere and its optical properties were reproducible. The gratings exhibited thermal stability up to 150°C because of their crosslinked structure, and are expected to be useful for device application.
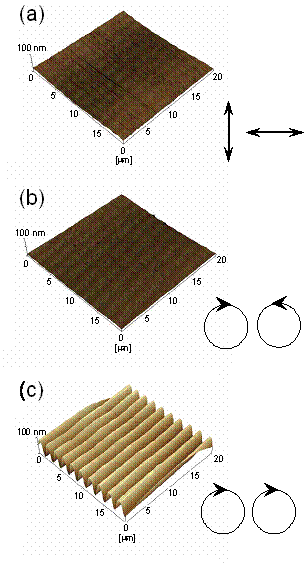
Before characterizing the diffraction and polarization conversion by the recorded gratings, the surfaces of the recorded gratings were observed with atomic force microscopy (AFM). Figsure 5(a) and 5(b) show the surfaces of the polarization holograms and revealed surface topologies with features of less than 4 nm by AFM. This means polarization analysis of the diffracted beams can be performed by assuming pure polarization gratings without topological relief and the above-mentioned theory is valid for our polarization gratings. In contrast, the surface relief gratings were clearly observed in the case of intensity holographic recording as shown in Figure 5(c). In the case of intensity holographic recording, the intensity of the interference light is modulated in space. Therefore, the density of the photocrosslinked compounds is spatially modulated and its density modulation stimulates to move the polymer. However, in the case of the polarization holographic recording, since the interference pattern of two coherent waves of equal amplitude and orthogonal polarizations has a constant intensity, the density of the crosslinked compounds are not modulated. The phase gratings recorded by means of the polarization holographic technique correspond to the pure polarization gratings by the reorientation of the mesogenic groups according to the polarization information of the interference beams illustrated in Figure 3.
|
|
|
Figure 5. Typical AFM three-dimensional view of (a), (b) polarization holographic recorded gratings and (c) intensity holographic recorded gratings on the photocrosslinkable polymer liquid crystal.
|
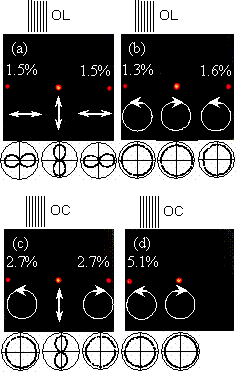
Figure 6 shows the typical examples of fundamental functions of resulting polarization gratings. The polar plots of each diffraction beam are represented at the bottom of the pictures of the diffraction patterns. For the OL polarization gratings [Figures 6(a) and 6(b)], the  first-order diffraction beams were linearly p-polarized when the reading beam was linearly s-polarized, while first-order diffraction beams were linearly p-polarized when the reading beam was linearly s-polarized, while 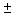 first-order diffraction beams were left-hand side circularly polarized when the reading beam was right-hand side circularly polarized. For the OC polarization gratings [Figures 6(c) and 6(d)], the + first-order diffraction beam was left-hand circularly polarized and the – first-order diffraction beam was right-hand circularly polarized when the reading beam was linearly s-polarized. When the reading beam was right-hand side circularly polarized, the + first-order diffraction beam was left-hand side circularly polarized, while the – first-order diffraction was invisible. These experimentally observed properties were consistent with the theoretical expectations, as summarized in Figure 4. The observed diffraction efficiencies are also represented in Figure 6. first-order diffraction beams were left-hand side circularly polarized when the reading beam was right-hand side circularly polarized. For the OC polarization gratings [Figures 6(c) and 6(d)], the + first-order diffraction beam was left-hand circularly polarized and the – first-order diffraction beam was right-hand circularly polarized when the reading beam was linearly s-polarized. When the reading beam was right-hand side circularly polarized, the + first-order diffraction beam was left-hand side circularly polarized, while the – first-order diffraction was invisible. These experimentally observed properties were consistent with the theoretical expectations, as summarized in Figure 4. The observed diffraction efficiencies are also represented in Figure 6.
|
|
|
Figure 6. Typical examples of the diffraction patterns passed through one-dimensional polarization gratings. In each picture, the diffraction efficiencies are shown at the top, the diffraction patterns are shown in the middle, and the polarization states are shown at the bottom. The polar plot for each diffraction beam was shown at the bottom of the picture.
|
The diffraction efficiencies under various conditions are theoretically given by Eq. (6), and their relationship is summarized as the following form:
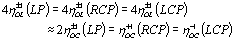 (7) (7)
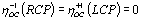 (8) (8)
The experimental results are in good agreement with the theoretical expectation described by Eqs. (7) and (8).
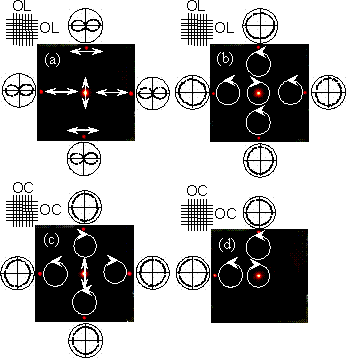
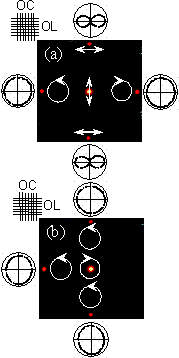
Two-dimensional crossed polarization gratings were fabricated using the same photocrosslinkable polymer liquid crystal by overwriting the polarization gratings at the same place. Figure 7 shows the diffraction patterns from the crossed gratings formed by overwriting the same polarization gratings, while Figure 8 shows the diffraction patterns from the crossed gratings formed by overwriting the two kinds of polarization gratings. The diffraction properties and their polarization conversion can be simply explained by considering the characteristics of the above-mentioned fundamental properties of the polarization gratings. The thermal stability of the polarization grating is very important in order to apply them to real optical devices. Our polarization gratings exhibited high thermal stability up to 150°C because of the photocrosslinked structure.
|
|
|
Figure 7. Diffraction patterns passed through the crossed gratings formed by overwriting the same polarization gratings.
|
|
|
|
Figure 8. Diffraction patterns passed through the crossed gratings formed by overwriting the two kinds of polarization gratings.
|
Conclusions
Highly stable one- and two-dimensional polarization gratings, which can control both polarization state and propagation direction of the laser beam, have been presented for a practical use. The characteristics of the resultant polarization gratings were well-explained by the Jones calculus. The high performance of our polarization gratings, which suggest that the choice of the photoclosslinkable liquid crystal is significant, originate in the regulated mesogenic molecules and photocroslinked structure.
Acknowledgements
This work was partially supported by the 21st century COE program and a Grant-in-Aid (NO.14550036) for Scientific Research from the Ministry of Education, Science, and Culture of Japan.
References
1. Polymers as Electronical and Photooptical Active Media, edited by V. P. Shivaev (Springer, Berlin, 1996).
2. T. Todorov, L. Nikolova and N. Tomova, “Polarization holography. 1: A New High-efficiency Organic Material with Reversible Photoinduced Birefringence”, Appl. Opt., 23 (1984) 4309-4312.
3. H. Ono, N. Kowatari and N. Kawatsuki, “Study on Dynamics of Laser-induced Birefringence in Azo Dye Doped Polymer Films”, Opt. Mater., 15 (2000) 33-39.
4. Y. Shi, W. H. Steier, L. Yu, M. Chen and L. R. Dalton, “Large Stable Photoinduced Refractive Index Cahnge in a Nonlinear Optical Polyester Polymer with Disperse Red Side Groups”, Appl. Phys. Lett., 58 (1991) 1131-1133.
5. P. Rochon, J. Gosselin, A. Natansohn and S. Xie, “Optically Induced and Erased Birefringence and Dichroism in Azoaromatic Polymers”, Appl. Phys. Lett., 60 (1992) 4-6.
6. Y. Wu, Y. Demachi, O. Tsutsumi, A. Kanazawa, T. Shiono and T. Ikeda, “Photoinduced Alignment of Polymer Liquid Crystals Containing Azobenzene Moieties in the Side Chain. 2. Effect of Spacer Length of the Azobenzene Unit on Alignment Behavior”, Macromolecules, 31 (1998) 1104-1108.
7. M. Schadt, K. Schmitt, V. Kozinkov and C. Chigrinov, “Surface-Induced Parallel Alignment of Liquid Crystals by Linearly Polymerized Photopolymers”, Jpn. J. Appl. Phys., Part 1, 31 (1992) 2155-2164.
8. N. Kawatsuki, H. Takatsuka, T. Yamamoto and O. Sangen, “Optical Anisotropy of Photoreacted Side-Chain Liquid-Crystalline Polymer Induced by Linearly Polarized UV Light”, J. Polym. Sci., Part A: Polym. Chem., 36 (1998) 1521-1526.
9. N. Kawatsuki, T. Yamamoto and H. Ono, “Photoinduced alignment control of photoreactive side-chain polymer liquid crystal by linearly polarized UV light”, Appl. Phys. Lett., 74 (1999) 935-937.
10. N. Kawatsuki, K. Goto, T. Kawakami and T. Yamamoto, “Reversion of Alignment Direction in the Thermally Enhanced Photoorientation of Photo-Cross-Linkable Polymer Liquid Crystal Films” Macromolecules, 35 (2002) 706-713.
11. L. Nikolova, T. Todorov, M. Ivanov, F. Andruzzi, S. Hvilsted and P. S. Ramanujam, “Polarization holographic gratings in side-chain azobenzene polyesters with linear and circular photoanisotropy”, Appl. Opt., 35 (1996) 3835-3840.
12. F. Ciuchi, A. Mazzulla and G. Cipparrone, “Permanent polarization gratings in elastomer azo-dye systems: comparison of layered and mixed samples”, J. Opt. Soc. Am., B 19 (2002) 2531-2537.
13. H. Ono, A. Emoto, F. Takahashi, N. Kawatsuki and T. Hasegawa, “Highly stable polarization gratings in photocrosslinkable polymer liquid crystals”, J. Appl. Phys., 94 (2003) 1298-1303.
Contact Details
|
Akira Emoto
Department of Electrical Engineering
Nagaoka University of Technology
1603-1, Kamitomioka, Nagaoka 940-2188
Japan
|
Hiroshi Ono
Department of Electrical Engineering
Nagaoka University of Technology
1603-1, Kamitomioka, Nagaoka 940-2188
Japan
E- mail: [email protected]
|
|
Nobuhiro Kawatsuki
Department of Material Science and Technology
Himeji Institute of Technology
2167 Shosha, Himeji 671-2201
Japan
E-mail: [email protected]
|
Emi Uchida
Department of Material Science and Technology
Himeji Institute of Technology
2167 Shosha, Himeji 671-2201
Japan
|
|
Masaomi Kuwabara
Department of Material Science and Technology
Himeji Institute of Technology
2167 Shosha, Himeji 671-2201
Japan
|
|
|