Powder Testing - A Case Study on Modern Tools for Hopper Design

Freeman Technology is a specialist company pioneering the measurement and understanding of powders and their flow properties.

Powder Testing - A Case Study on Modern Tools for Hopper Design

Founded in 1989, the company developed the novel, patented technology that forms the core of its Powder Rheometer system at its design and manufacturing center in Gloucestershire, UK where all manufacturing takes place in an ISO 9001:2008 accredited environment. Research into understanding powder behavior is central to the company's business strategy.

Freeman Technology's business is researching powder behavior and designing instrumentation for powder characterization.

The FT4 Powder Rheometer is a universal powder tester that is really three instruments in one – combining a powder rheometer with a shear cell capability and a compression tester. This allows a comprehensive characterization of powders of all types, reflecting the complexity of powders in contrast to traditional single number assessments of flowability.

Hopper Design and Powder Testing

Although there are well-established methodologies for hopper design, many process engineers are uncertain as to how to measure powders in a prescribed way, extract the necessary parameters from recorded data, and successfully apply them.

As a result, hopper design and the powder testing associated with it is often outsourced to specialists. This incurs significant cost and undermines the operating company's ability to troubleshoot and re-use or retrofit equipment for alternative materials or applications.

The advent of modern, automated powder testing systems has simplified measurement, making it easier for users who are not instrument specialists to precisely determine the parameters required for hopper design.

Recently released software for the FT4 Powder Rheometer guides engineers through the established methodologies, showing how to use measurements to generate a specification that will operate in an acceptable way. Together these developments bring hopper design easily within the remit of the majority of process engineers, offering an opportunity to reduce costs and gain a better understanding of the factors influencing performance.

Here we examine the issues surrounding hopper design and show, using a worked example, how FT4 software simplifies the whole process – from powder measurement through to specification.

The Basics of Hopper Design

In this paper the term 'bin' refers to the section of a storage vessel with parallel-sided walls, 'hopper' is the angled portion below. A storage vessel or silo, therefore, consists of both bin and hopper.

Many different shapes of hopper and bin are routinely used but in each case, the design intent is the same: reliable, steady powder discharge, at the required rate. Selecting an appropriate outlet size and hopper half-angle, the degree of incline from the vertical, of the hopper walls, achieves this aim. The resultant flow regimes can be broadly divided into two – mass flow and core or funnel flow.

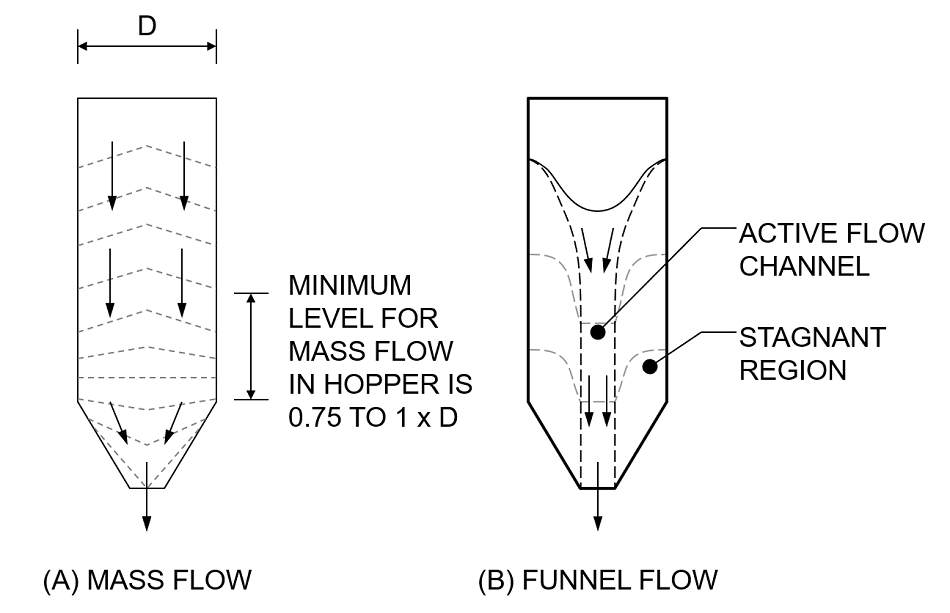
Figure 1. Flow regimes for powders discharging from a storage silo.

Half angle strongly influences the flow mode or regime that develops within the silo (see figure 1). With mass flow (the preferred option for the majority of applications) all of the powder is in motion as a material is withdrawn at the exit, producing a 'first in, first out' regime. Flow tends to be relatively consistent and the full capacity of the bin is used. With funnel flow, on the other hand, there is an active channel down the center of the vessel but powder stagnates along with the 'hopper' and bin walls. Steeper hopper walls – smaller hopper half angles – encourage mass as oppose to funnel flow.

Funnel flow produces 'last in, first out' powder delivery and a greater likelihood of operational problems such as ratholing, segregation, and flooding. Rat holing is where a central void develops above the discharge outlet in place of the active flow channel. The collapse of rat holes can cause significant mechanical damage and/or excessive aeration of the powder. More generally, aeration in the active flow channel encourages flooding (where the powder becomes fluid-like and flows uncontrollably) and segregation (the separation of particles on the basis of size), both of which are undesirable. While these operational disadvantages discourage the use of funnel flow it can be the preferred choice when building height is limited for example. Funnel flow designs can be short and wide because the hopper sides are shallowly angled while mass flow units accommodating an equivalent volume tend to be taller with a smaller cross-sectional area.

Powder Flow Behaviour in a Bin and Hopper

Powder flow behavior in a bin and hopper is governed by:

• The shear properties of the powder – how easily the particles move relative to each other
• Wall friction – how easily the powder flows over the inner surface of the container
• Compressibility – how the application of consolidating stress changes bulk density

These variables define how the powder will behave in the hopper when consolidated by the weight of the material in the bin. Potentially a stable arch can form across the hopper outlet (figure 2), and if this is strong enough to support the rest of the powder in the vessel then discharge ceases. For any given combination of powder and material of construction, hopper half-angle and outlet size determine whether a stable arch can form. In the 1960s Jenike carried out a detailed flow analysis based on this flow/no-flow condition, to develop a design methodology that remains the standard.

Figure 2. The formation of a stable arch that prevents powder flow depends on the relative size of forces acting within the hopper

Determining Flow Function (FF) and Flow Factor (ff)

A full description of the associated mathematical analysis lies beyond the scope of this paper but in summary, the technique involves determining two parameters: flow function (FF) and flow factor (ff).

Flow function depends purely on the shear strength of the powder, which is measured as a function of applied normal stress using shear cell apparatus. The torque or force required to shear a consolidated powder bed across a plane is accurately determined to generate yield loci for the material from which FF is derived. Details on shear cell testing methodology and the associated Mohr's circle analysis are available elsewhere.

Flow factor, ff, in contrast, depends on the characteristics of the hopper material of construction, shape - as well as those of the powder, and is, for any specific hopper configuration, a function of hopper half angle, wall friction and material bulk strength.

A plot of FF and ff is shown in figure 3. It is clear that both parameters describe relationships between shear strength and consolidating stress, one for the material itself (FF), the other for the material within the specific hopper environment (ff). The point at which these two curves intersect gives the value of stress in a hypothetical arch at the transition point from flow to no flow. Outlet size is calculated from this value through a simple force balance on the arch.

Figure 3. A plot of FF and ff showing the intersect point defining the flow/no flow transition

It is important to recognise from this analysis that any change in the FF or ff will alter the critical dimensions of the hopper. If the material of construction, shape or half angle of one hopper is different from that of another, then a different outlet size will be needed to achieve flow, for the same powder.

If the intent is to use a storage silo for a powder different from the one for which it was designed, then this will alter FF (and ff) and so half angle and outlet size may or may not be adequate. Both these conclusions are fairly obvious. However, what is perhaps less well-understood is that FF and ff may change, for a given material, depending on in-process conditions and the powder properties.

If the material segregates, for example, the hopper may have to cope with slugs of finer and coarser material, which may be more or less cohesive respectively. Moisture level too can cause a significant change in shear strength as can storage time.

If the material is allowed to consolidate under its own weight for a significant period then shear strength can rise significantly (time consolidation). Repeated testing under different conditions allows the designer to assess sensitivity to such changes. The choice is then either to specify on the basis of the worst expected case, or install upstream measures to avoid variability that will compromise hopper operation.

Case Study: Determining Half Angle and Outlet Diameter for a Conical Hopper

The new software for the FT4 guides the user through measurement, data workup and the design methodologies developed by Jenike (figure 4); in this example the design is for potato flour. Automation of every step facilitates precise powder testing and generation of an acceptable design...

Want to know more? Click here to read the full article.

This information has been sourced, reviewed and adapted from materials provided by Freeman Technology.

For more information on this source, please visit Freeman Technology.