Mar 23 2017
 This is a schematic of molecules in a confined liquid. Credit: Stevenson, Curro, McCoy
This is a schematic of molecules in a confined liquid. Credit: Stevenson, Curro, McCoy
Polymers are used for countless applications, and the most vital property that dictates which polymer is selected for a given application is its "glass transition temperature."
A number of industrial polymers find it impossible to crystallize as they possess an irregular molecular structure. As a polymer material cools from a temperature higher than its glass transition temperature, it morphs from a liquid to a glass after reaching the transition temperature.
While a liquidlike, amorphous structure is possessed by a polymer material in its glassy state, the mobility of the molecules is so low that they are fundamentally frozen. A number of hard plastics are actually glassy.
For instance, polystyrene has a glass transition temperature of almost 100 oC - at room temperature it acts like a solid material. However, the mechanical properties of polystyrene change drastically as the temperature of polystyrene reaches the glass transition temperature.
This makes the ability to approximate glass transitions for confined geometries in polymers highly desirable. A group of researchers from the University of New Mexico and New Mexico Institute of Mining and Technology have recently reported their development of a simple formula to do just that in the recent issue of the Journal of Chemical Physics, from AIP Publishing.
With the development of nanotechnology, polymers have found many applications that require their use in 'confined geometries' such as narrow channels, small pores, and thin films.
John Curro, Adjunct Professor, New Mexico Institute of Mining and Technology
Experiments performed over the past two decades have demonstrated that when polymers are used in a confined geometry, their glass transition "isn't necessarily the same as for the corresponding 'unconfined' or bulk polymer," Curro said. "It's usually lowered, as is the case for free-standing films with two free surfaces, but it can also increase for liquids against strongly attracting substrates."
The shift in glass transition sensitively relies on film thickness -- a greater effect is obtained when the film is thicker. "This shift can be extraordinarily large," Curro said. "For example, the glass transition temperature of a 20-nanometer polystyrene film has been measured as much as 70 C lower than bulk polystyrene. Clearly, this thin film of polystyrene is no longer a hard plastic material."
As far as potential applications, "the fact that polymer properties in confined geometries are different than in bulk could have important implications for photolithography, nanocomposites, micromachines, and lab-on-a-chip devices," Curro said.
Why is the glass transition of a confined polymer different from that of its corresponding bulk material?
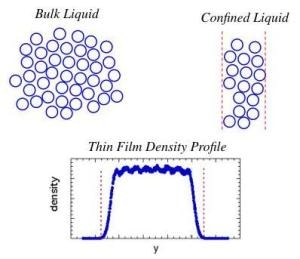
We hypothesized that it's due to a density effect. In an unconfined bulk liquid, the density is constant throughout the sample. By contrast, a confined liquid's density of molecules is nonuniform because of constraints imposed by geometry.
John Curro, Adjunct Professor, New Mexico Institute of Mining and Technology
A freestanding film's density, for instance, is in fact zero at the two surfaces but within the center it increases to near the bulk density.
"Since the glass transition temperature depends strongly on density, we expect the local glass transition temperature to likewise vary throughout the film," Curro said. "In a lab experiment, the measured glass transition temperature represents the average response of the material within the film. The average density of a freestanding film is generally different than its bulk density, and it follows that the glass transition temperatures will also be different."
Hence, the group investigated whether a confined liquid’s glass transition temperature would be the same as a hypothetical bulk polymer - not at its usual bulk density, but instead at a density equal to the average density of the confined polymer.
The researchers wanted to measure both the glass temperature and the density profile on the same thin film in order to put it to test. It will indeed be difficult to carry out such measurements in the laboratory.
"Our approach was to use 'molecular dynamics' computer simulations to study thin liquid films consisting of short chain molecules," Curro said. "We also performed computer simulations of the corresponding bulk system. This allowed us to compare the glass transition temperatures of thin films of various thicknesses with the bulk glass transition temperature on the same model chains."
An idealized bead-spring model of 10 beads was used by the team to represent the molecules in order to obtain computational efficiency. By doing so, they "established a connection between the glass transition temperatures of a polymer in a constrained geometry and the corresponding bulk polymer," Curro said.
This allowed us to develop a simple formula to estimate the glass transition of a confined liquid from the bulk glass transition temperature and a knowledge of the density profile of the confined system.
John Curro, Adjunct Professor, New Mexico Institute of Mining and Technology
It is also essential to note that the results obtained by the group only apply to small molecule glasses and low molecular weight polymers.
"Subtle molecular weight effects are observed experimentally at high molecular weights when the average chain size is comparable to the film thickness, so high molecular weight will be a topic for future investigations," Curro said.