Dec 10 2018
The atoms in a crystalline solid generally form an ordered lattice. Such a crystalline solid reacts elastically to slight deformations: upon removing the applied strain, the macroscopic stress, in addition to the microscopic configuration of the atomic lattice, returns back to the original state.
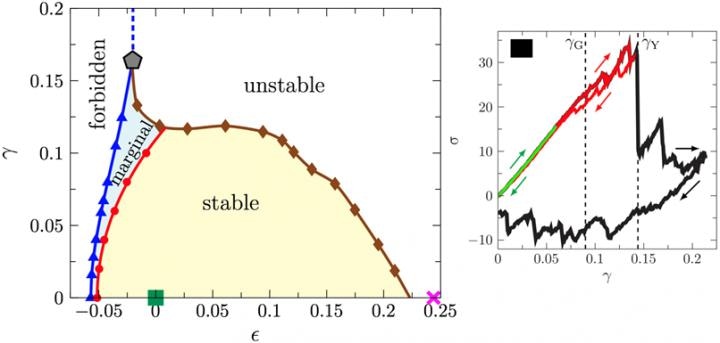Left: Stability-reversibility map of hard sphere amorphous solids, represented in terms of volume and shear strains. Right: Typical stress-strain curves which show the reversible (green) and partially reversible (red) behaviors. (Image credit: JIN Yuliang)
In contrast, if a material does not go back to its original state, it behaves plastically. Generally, plasticity takes place only when the deformation is adequately large.
To address this question, Dr JIN Yuliang from the Institute of Theoretical Physics (ITP) of the Chinese Academy of Sciences, along with his collaborators, used a numerical model system to thoroughly analyze the mechanical characteristics of amorphous solids.
While microscopic configurations can be irreversible, macroscopic properties like strain and stress are reversible when a small deformation is released. The work required to shift between before-perturbation and after-perturbation configurations is insignificant. This type of amorphous solid is referred to as marginally stable and arises from what is known as a Gardner transition, as predicted lately by mean-field theory.
A stability-reversibility map of hard-sphere amorphous solids was further established by the scientists. This map unifies mechanical behaviors including plasticity, elasticity, jamming, and yielding.
In accordance with the stability-reversibility map, an amorphous solid possesses two characteristic behaviors, which is dependent on the level of volume and shear strains. The amorphous solid in the stable region is actually reversible and elastic, similar to crystals. On the other hand, in the marginally stable region, elasticity is inevitably combined with plasticity, even for extremely small deformations. Moreover, a marginally stable amorphous solid is just partly reversible.
The research demonstrates that there is a need for a more complete elastic theory—one that can precisely integrate amorphous solids. It also offers a significant understanding of the design of sophisticated mechanical materials like metallic glasses.
Study collaborators include Dr Hajime Yoshino of Osaka University, Japan; Dr Pierfrancesco Urbani of Université Paris Saclay, France; and Dr Francesco Zamponi of École Normale Supérieure, France.